SFM Learner 2017
SFM Learner 2017
Zhou T, Brown M, Snavely N, et al. Unsupervised learning of depth and ego-motion from video
为单目深度估计与相机姿态估计提出完全无监督的学习框架;
单视图深度估计与多视图位姿分别构建网络,将图像变换到目标视图上以构建损失,并根据此损失训练网络
方法
从无标签视频序列中联合训练单视图深度 CNN 和相机位姿估计 CNN。这两个模型合并训练但可分开独立使用,模型适用于刚体场景。
将视图合成作为监督
深度和位姿估计 CNNs 监督信号主要为新合成的视图:给定一副图像,合成该图像在另外一个视角的图像,合成过程由后一节提出的完全可微 CNN 实现。
\(<I_1,\cdots,I_N>\)
为训练中使用的图像序列,其中 \(I_t\)
为目标视图,并假设源图像为 \(I_s(1\le s\le
N,s\neq t)\) ,那么视图合成的优化目标为: \[
\mathcal{L}_{vs} = \sum_s \sum_p \vert I_t(p)-\hat I_s(p) \vert
\] 其中 \(p\)
表示图像中每一个像素,\(\hat I_s(p)\)
由 \(I_s(p)\) 根据预测的深度图 \(\hat D_t\) 以及 \(4 \times 4\) 的相机变换矩阵 \(\hat T_{t\rightarrow s}\)
扭曲得到。这篇文章的视图合成监督信号不需要已知的相机位姿,因为相机位姿估计是整个网络框架的一部分,同样要被优化。
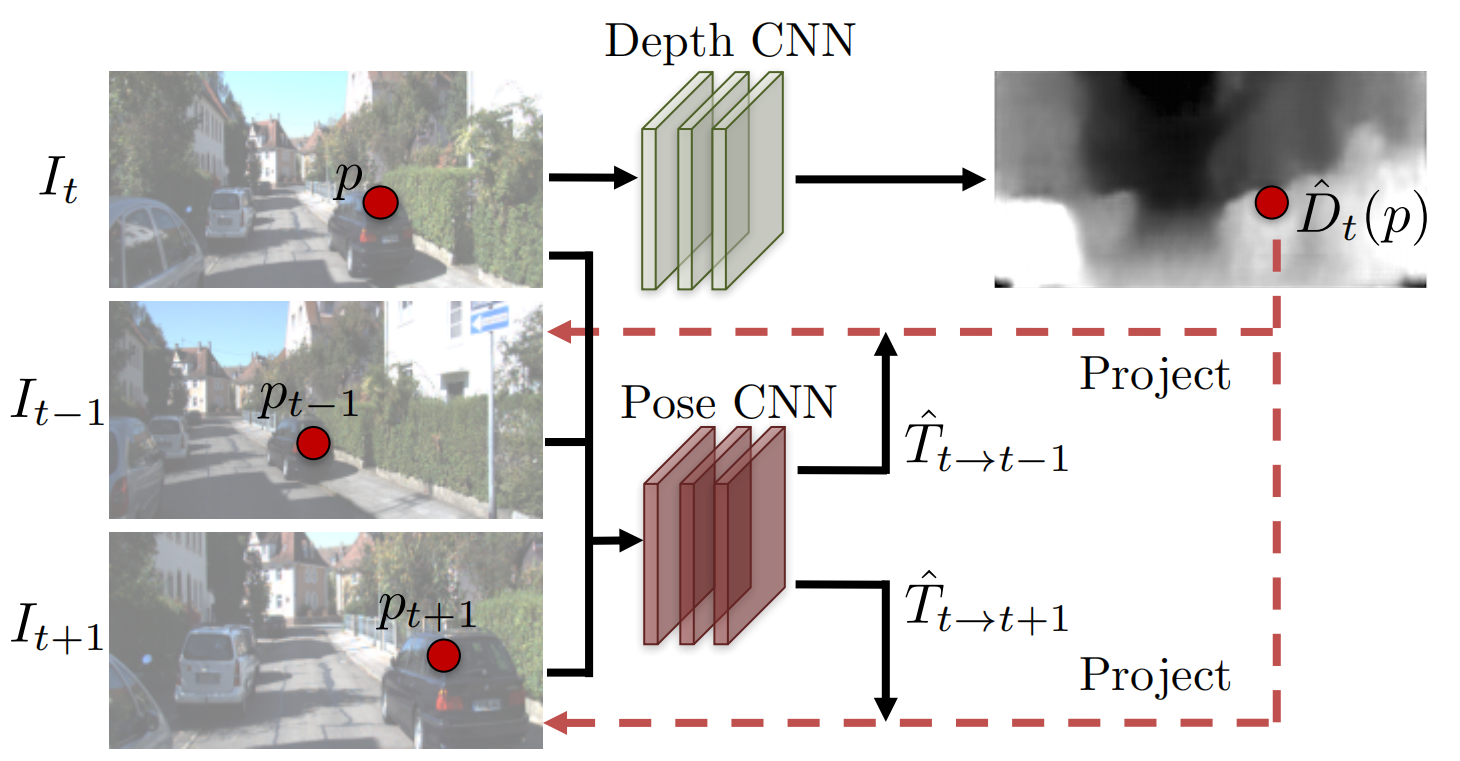
这个步骤其实就是将 \(I_s\) 扭曲为 \(I_t\) 并计算光度误差,为了使网络能够训练,即误差传递,所以扭曲变换需要是可微的,即下面的可微渲染。
基于深度图的可微渲染
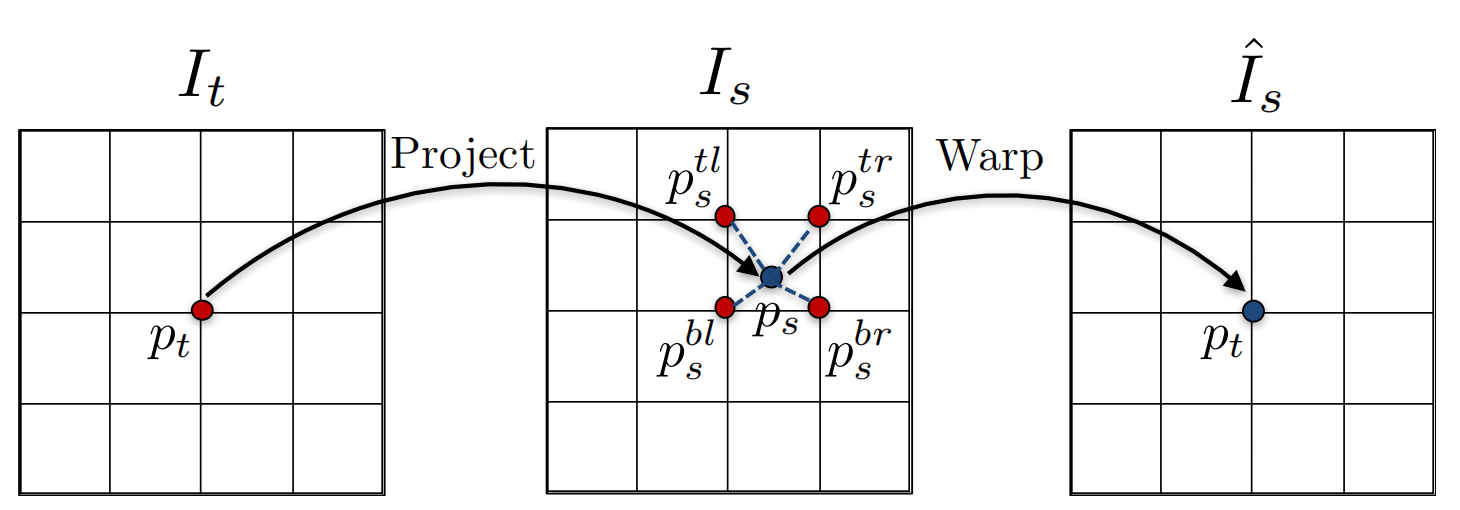
根据目标视图 \(I_t\) 的深度图 \(\hat D_t\) 以及位姿估计网络得到的目标视图到源视图的变换矩阵 \(\hat T_{t\rightarrow s}\),可以将 \(I_s\) 变换为 \(I_t\),令 \(p_t\) 为目标视图 \(I_t\) 上的像素坐标,它在源视图 \(I_s\) 对应像素的坐标为: \[ p_s \sim K\hat T_{t\rightarrow s}\hat D_t(p_t)K^{-1}p_t \] 这里得到的 \(p_s\) 的连续的,为了获得 \(I_s(p_s)\) 则需要对其进行采样即插值得到 \(\hat I_s(p_t)\)。文章中用的是双线性插值表示如下: \[ \hat I_s(p_t) = I_s(p_s) = \sum_{i\in\{t,b\},j\in\{l,r\}} w^{ij}I_s(p_s^{ij}) \] 其中 \(w^{ij}\) 是线性插值的权重,满足 \(\sum_{ij} w^{ij} = 1\)
具体微分步骤见论文 M. Jaderberg, K. Simonyan, A. Zisserman, et al. Spatial transformer networks. 2015
模型限制
视图合成中的优化目标隐含表示:
- 目标场景是静态的,没有移动物体
- 目标视图与源视图之间没有遮挡
- 物体表面满足 Lambertian 反射,即理想漫反射模型,以使得光度误差有意义
为了使得网络更具鲁棒性,文章额外训练了一个 explainability prediction network,该网络将深度和位姿联合起来,为每一个目标-源像素对输出一个权重 \(\hat E_s\),基于此,视图合成误差表示为: \[ \mathcal{L}_{vs} = \sum_s \sum_p \hat E_s(p)\vert I_t(p)-\hat I_s(p) \vert \] 直接对上式训练会导致 \(\hat E_s\) 总是预测为 0,介于此,增加 \(\hat E_s\) 的正则化项 \(\mathcal{L}_{reg}(\hat E_s)\),\(\mathcal{L}_{reg}(\hat E_s)\) 为 \(\hat E_s\) 与 \(\mathbf 1\) 的交叉熵,以此让网络倾向于将 \(\hat E_s\) 预测为非零值,因为在理想条件下目标视图于源视图像素是能一一对应的,即 \(\hat E_s\) 全部为 1。
克服梯度局限性
\(\mathcal{L}_{vs}\) 的梯度主要由 \(I_t(p)\) 与 \(I_s(p_s)\) 周围四个像素的差提供,在缺少纹理的环境中以及预测误差较大的情况下将抑制训练,为此有两个策略来解决:
- 使用 encoder-decoder 网络结构,使得深度网络具有一定瓶颈以隐式约束输出达到全局平滑,并促使梯度从有意义的区域向四周传播
- 显示地增加多尺度和平滑误差以允许梯度从更大的区域获得
文章中使用第 2 种策略,因为它对架构不敏感。
针对平滑,最小化深度图二阶梯度的 L1 范式,【对深度图平滑是否可以平滑相机位姿预测结果】
最后的误差表示为: \[ \mathcal L_{final} = \sum _{l} \mathcal L_{vs}^l + \lambda_s \mathcal L_{smooth}^l + \lambda_e \sum_s \mathcal L_{reg}(\hat E_s^l) \] 其中 \(l\) 表示尺度,\(\lambda_s,\lambda_e\) 分别为平滑和正则误差的权重。
网络结构
网络的具体信息可查看官方代码
单视图深度
使用 encoder-decoder 架构并具有跳跃连接和多尺度的 DispNet,文章尝试了将多个视图传入网络,但并没有提高网络效果。
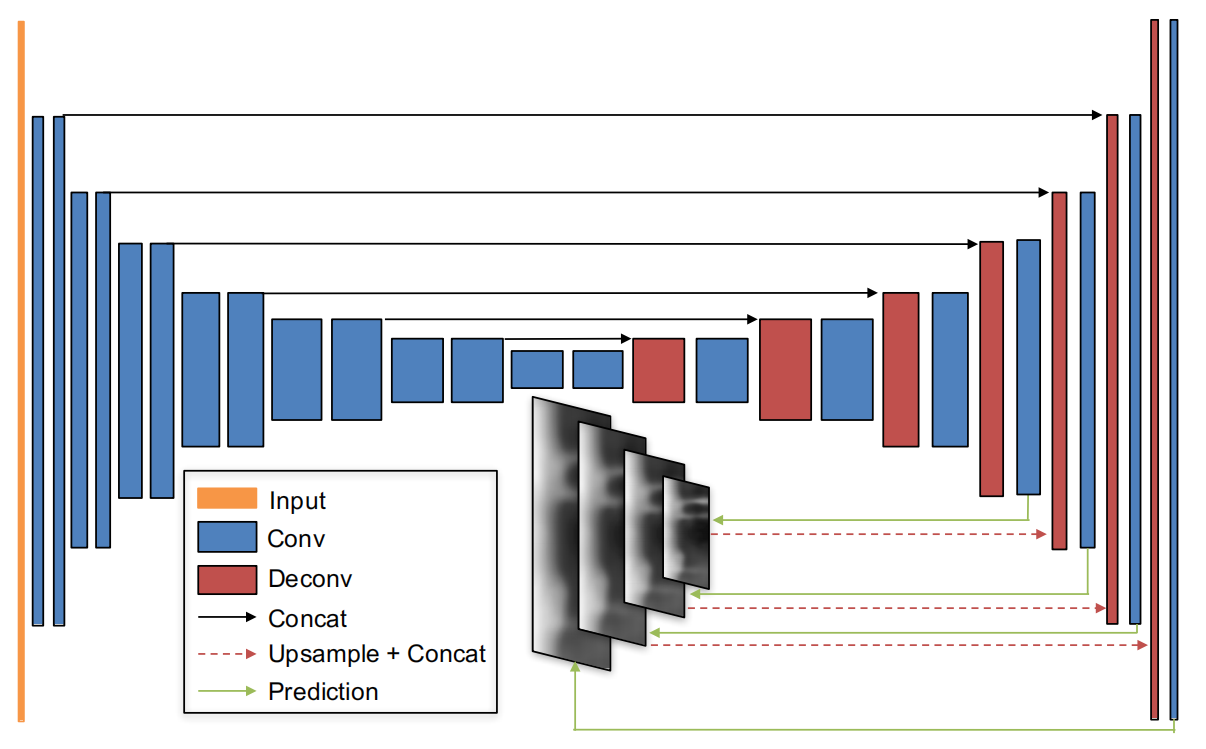
位姿
位姿网络的输入是目标视图和所有源视图沿着颜色通道的拼接。输出目标视图与所有源视图的相对位姿
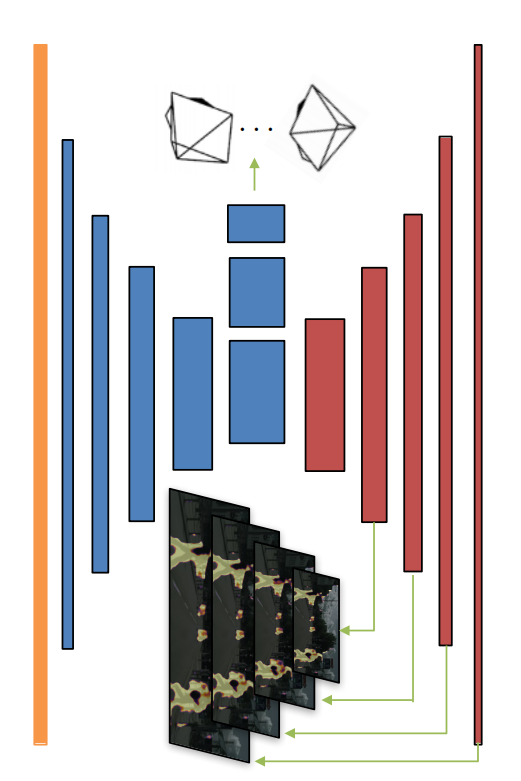
可解释掩模
上图前五层位姿网络和可解释掩模网络是共用的,上图红色部分是可解释掩模网络的。
讨论
方法存在的问题:
- 没有显示处理遮挡和物体运动
- 需要知道相机内参,不能完全随便拿一段视频训练
- 使用深度图表示三维,未来可以使用体素表示