【报告】相机位姿估计与点云优化
一、 研究问题
在基于视觉的三维重建算法(如 Structure From Motion, SFM1)以及同时定位与地图构建(Simultaneous localization and mapping, SLAM23)等涉及立体视觉的理论研究中,需要通过相机成像模型及特征点匹配等理论恢复相机位姿以重构三维场景,即目标点云的生成。
相机的位姿估计指从若干给定的图像中恢复相机的运动(位姿),进而恢复目标的三维结构(点云)。相机运动(位姿)即相机的外部参数,是世界坐标系到相机坐标系的变换,包含旋转和平移,即欧式变换。相机成像模型如下: \[ ZP_{uv} = Z \left[ \begin{matrix} u \\ v \\ 1 \end{matrix} \right] = K(RP_w+t) = KTP_w \tag{1.1} \]
其中 \(Z\) 为世界坐标系下目标点 \(P_w\) 的 z 轴坐标,\(K\) 为相机内参,可通过张正友标定法4确定,\(R,t\) 为世界坐标系到相机坐标系的变换,可以使用矩阵 \(T\) 表示,\(P_{uv}\) 代表像素坐标系,\(u,v\) 为像素坐标。这里目标为通过一些约束估计相机外参 \(R,t\) 。获取相机位姿后便可以进一步得到目标的三维点云。
二、 研究现状
三维重建相关的算法中,许多通过图像信息恢复三维结构。图像信息主要由特征点表示,通过特征点可以构建图像间的联系,进一步可以得到目标的三维信息。特征点指的是图像中具有代表性的点,反映图像的局部特征。代表性的图像特征提取算法有:SIFT5、SURF6、ORB7 等。这一类算法提取的特征点具有很强的不变性,如尺度不变性、光照不变性、旋转不变性等,并高效地表达图像的局部特征。特征点包含关键点及对应的描述符,关键点指特征点在图像的具体坐标,描述符则体现关键点的局部特征,为不同图像中特征的匹配提供支持。特征匹配是确定图像间关联关系的重要步骤,但由于特征点一般数量众多,特征匹配带来的资源消耗也十分大,快速最邻近算法(FLANN)8为大规模匹配作了优化。
在单目视觉中通过图像间的像素坐标匹配建立运动关系,可将问题转换为利用两组 2D 匹配对估计相机位姿,这类问题可通过对极几何解决。对极几何本质上是三维空间目标点和两相机中心共面的约束,由本质矩阵和基础矩阵表达,这两个矩阵蕴含了相机的运动,可以使用八点法9或者五点法10求解 \(R,t\)。但本质矩阵(或基础矩阵)具有尺度等价性,从而它得到的 \(R,t\) 也具有尺度等价性。旋转矩阵本身具有单位正交的约束,但分离得到的 \(t\) 具有尺度等价性,这是单目视觉的尺度不确定性的主要原因。得到两幅图像之间的运动之后可通过三角测量获得特征点的空间位置,估计目标点云,但仍然是尺度不确定的。
深度相机(RGB-D)通过红外结构光或“Time Of Flight”原理获得目标深度信息,从而直接得到目标的 3D 信息,是尺度确定的。从而相机的运动可以从两组 3D 匹配点中恢复,可以使用迭代最近点(Iterative Closest Point,ICP)求解。但 RGB-D 相机存在测量范围窄,噪声大,易受日光干扰等问题,一般适用于室内。
双目相机也可得到深度信息。它由两个单目相机组成,这两个相机的距离称为基线,通过基线以及视差图计算每一个像素的空间位置。双目相机比 RGB-D 相机具有更好的适用性,但视差图的计算量是巨大的,所以双目相机的主要问题在于如何加速计算以节约资源。
当知道空间点的三维坐标以及它们在图片上的投影位置时估计相机位姿,这类问题称为 PnP(Perspective-n-Point)问题。其中空间点的三维坐标可以通过三角测量或者 RGB-D 相机得到。PnP 克服了对极约束中尺度的不确定,是一种主要的姿态估计方法。PnP 问题求解有许多方法,如利用三对点对求解的 P3P11,当目标为平面时还可以使用直接线性变换(DLT),还有 EPnP (Efficient PnP)12等。这些方法对匹配点的精度要求十分高,但在实际情况中虽然可获得很大数量的匹配点对,但每个点对都存在一定误差,即存在噪声,而光束法平差(Bundle Adjustment,BA)通过构建非线性最小二乘问题对位姿和点云优化,具有很好的鲁棒性,在匹配点数量众多的情况下效果很好,所以这里讨论 BA 的求解方法。
三、解决方案
光束法平差13,Bundle Adjustment 是使用非线性优化求估计位姿,以及优化空间点位置的方法。这一章节先介绍非线性优化的相关理论,然后通过相机成像模型构建重投影误差,从而建立优化函数。并使用李代数将问题转换为无约束优化问题。
3.1 非线性最小二乘
经典的非线性最小二乘问题可以表达为: \[ \min_{\pmb x} F(\pmb x) = \frac{1}{2} \vert\vert f(\pmb x) \vert\vert_2^2 \tag{3.1.1} \] \(f(\pmb x)\) 可以是向量函数,非线性最小二乘目标是找到 \(\pmb x\) 使得目标函数 \(F(\pmb x)\) 到达最小值。函数极值问题即求解 \(\frac{dF(x)}{dx}=0\),满足这个条件的解可能是极大值、极小值或者是鞍点,这个方程的难解程度依赖于 \(f(\pmb x)\) 本身的特点。此外,还可利用迭代求解:
- 确定初值 \(x_0\)
- 对于第 k 次迭代,搜寻一个增量 \(\Delta x_k\),满足 \(\vert \vert f(x_k+\Delta x_k) \vert \vert_2^2\) 达到最小
- 迭代停机条件:当 \(\Delta x_k\) 足够小时,停止
- 否则进行更新:\(x_{k+1} = x_k + \Delta x_k\),并返回步骤 2
在迭代过程中,不断更新 \(x\) 使得函数值越来越小,即将求导问题转换为 \(\Delta x_k\) 的确定问题。但这里停机时候的解并不一定是全局最优的,这依赖于初值的确定,不好的初值可能使得迭代陷入局部最小值,所以对于此类非线性优化问题初值的选择十分重要。
\(\Delta x_k\) 的选择可以使用高斯牛顿法确定。将 \(f(\pmb x)\) 进行一阶泰勒展开,可得: \[ f(x+\Delta x) \approx f(x) + J(x)\Delta x \tag{3.1.2} \] 其中 \(J(x)\) 为 \(f(x)\) 关于 \(x\) 的雅可比矩阵,根据前面确定的迭代流程,给定 \(x\) 需要要找到 $x $ 使得 \(\vert \vert f(x+\Delta x) \vert \vert_2^2\) 达到最小,将式 3.1.2 带入 式 3.1.1 可得: \[ \Delta \hat x = \arg \min_{\Delta x} \frac{1}{2} \vert \vert f(x)+J(x)\Delta x \vert\vert_2^2 \tag{3.1.3} \] 这里 \(x\) 是已知项,即 \(x_k\) 。所以这是一个线性最小二乘问题,易知该函数是一个凸函数,只需要对 \(\Delta x\) 求导,并令其等于 0 即可。可得: \[ J(x)^Tf(x) + J(x)^TJ(x) \Delta x = 0 \tag{3.1.4} \] 进一步可得: \[ \begin{align} H(x)\Delta x &= g(x) \tag{3.1.5}\\ H(x) &= J(x)^TJ(x) \\ g(x) &= - J(x)^Tf(x) \end{align} \] 高斯牛顿法的核心为求解式 3.1.5,线性方程组可以使用很多方式求解,对于不同的 \(H(x)\) 可以采取不同的求解方式,以提高求解速度。高斯牛顿法总结如下:
- 确定初值 \(x_0\)
- 对于第 k 次迭代,求解当前的雅可比矩阵 \(J(x_k)\) 并构建方程 \(H(x_k)\Delta x_k = g(x_k)\)
- 迭代停机条件:当 \(\Delta x_k\) 足够小时,停止
- 否则进行更新:\(x_{k+1} = x_k + \Delta x_k\),并返回步骤 2
高斯牛顿法存在步长可能过大的问题。一种改进为列文伯格-马夸尔特(Levenberg-Marquardt)14方法,它采用了动态步长,很大程度上改良了高斯牛顿法。
3.2 李群李代数
在 3.1 节介绍的为无约束非线性最小二乘算法,但在光束法平差中需要对旋转矩阵求导并更新,旋转矩阵具有内在的约束,需要保证其为单位正交阵。旋转矩阵没有加法定义,即两个旋转矩阵相加并不是旋转矩阵,定义在旋转矩阵上有意义的运算为乘法运算。
三维旋转矩阵构成特殊正交群 SO(3),三维旋转加平移则构成特殊欧式群 SE(3),定义如下: \[ \begin{align} \text{SO}(3) &= \{R\in \mathbb R^{3\times 3}|RR^T=\pmb I,\det(R)=1 \} \tag{3.2.1}\\ \text{SE}(3) &= \Big\{T= \left[ \begin{matrix} R & t \\ \pmb 0^T & 1 \end{matrix} \right] \in \mathbb R^{4\times 4}| R\in \text{SO(3)}, t\in \mathbb R^3 \Big\} \tag{3.2.2} \end{align} \] SO(3)、SE(3) 都属于李群,每一个李群都有对应的李代数,李代数描述了李群的局部性质,是其正切空间的表示。SO(3)、SE(3) 对应的李代数表示为 \({\frak{so}}(3)\)、\({\frak{se}}(3)\),李群与李代数之间可以通过指数映射和对数映射相互转换。将旋转角度约束在 \(\pm \pi\) 之内,此映射便为一个双射。 \[ \begin{align} R = {\rm exp}(\phi^{\wedge})&,\phi^{\wedge} = \log(R) \tag{3.2.3}\\ T = \exp (\xi^{\wedge})&,\xi^{\wedge} = \log (T) \tag{3.2.4}\\ \end{align} \] 其中: \[ \begin{align} \phi &= [\phi_1 \quad \phi_2 \quad \phi_3]\in {\frak so}(3) \\ \phi^{\wedge} &= \left[ \begin{matrix} 0 & -\phi _3 & \phi_2 \\ \phi_3 & 0 & -\phi_1 \\ -\phi_2 & \phi_1 & 0 \end{matrix} \right] \tag{3.2.5}\\ \xi &= [\rho^T\quad \phi^T] \in {\frak se}(3) \tag{3.2.6}\\ \xi^{\wedge} &= \left[ \begin{matrix} \phi^{\wedge} & \rho \\ \pmb 0^T& 0 \end{matrix} \right] \tag{3.2.7}\\ \rho &\in \mathbb R^3 \end{align} \] \({\frak so}(3)\) 本质上是旋转向量组成的空间,旋转向量是无约束的。\({\frak se}(3)\) 则可以理解为平移向量和 \({\frak so}(3)\) 的结合。将李群转换到李代数就可以构建无约束优化问题。在优化问题求导是重要的步骤,这里讨论对空间施加一个变换,考虑对变换的导数。李群没有加法定义,所以不能使用导数定义求导,李群的求导需要使用扰动模型,对李群左乘或者右乘一个微小扰动 \(\exp(\delta^{\wedge})\),然后计算变化量 \(\epsilon\) 对扰动 \(\delta\) 的导数,如下: \[ \begin{align} TP + \epsilon &= \exp (\delta^{\wedge})TP \tag{3.2.8} \\ \delta &\in {\frak se}(3) \end{align} \]
由式 3.2.8、3.2.7 ,并根据左扰动模型可以得到 \(TP\) 对微小变换的导数为: \[ \begin{align} \frac{\partial TP}{\partial \delta} &= \frac{\partial \epsilon}{\partial \delta} \\ &= \frac{\partial (\exp (\delta^{\wedge})TP - TP)}{\partial \delta} \\ &= \frac{\partial ((\pmb I + \delta^{\wedge})TP - TP)}{\partial \delta}\\ &= \frac{\partial (\delta^{\wedge}TP)}{\partial \delta} \\ &= \frac{\partial \left[ \begin{matrix} \phi^{\wedge} & \rho \\ \pmb 0^T& 0 \end{matrix} \right] \left[ \begin{matrix} Rp+t \\ 1 \end{matrix} \right] }{\partial \delta} \\ &= \frac{\partial \left[ \begin{matrix} \phi^{\wedge}(Rp+t)+\rho \\ \pmb 0^T \end{matrix} \right] }{\partial [\rho \quad \phi^{\wedge}]}\\ &= \left[ \begin{matrix} \pmb I & -(TP)^{\wedge} \\ \pmb 0^T& 0 \end{matrix} \right] \tag{3.2.9} \end{align} \] 3.1 节非线性优化模型中,对变量求导之后的更新步骤使用的是加法更新。在扰动模型中,由式 3.2.8 可知应该使用 \(\exp(\delta^{\wedge})T\) 更新矩阵 \(T\),即: \[ T_{k+1} = \exp(\delta^{\wedge})T_k \tag{3.2.10} \]
3.3 光束法平差
根据相机成像模型有: \[ \begin{align} s_i \pmb u_i &= KTP_i \tag{3.3.1}\\ \pmb u_i &= \left[ \begin{matrix} u_i & v_i & 1 \end{matrix} \right]^T \\ P_i &= \left[ \begin{matrix} X_i & Y_i & Z_i & 1 \end{matrix} \right]^T \end{align} \] 式 3.3.1 中 \(\pmb u_i\) 第 i 个匹配的像素坐标,\(P_i\) 为对应的空间点。由于相机位姿 \(T\) 未知,且空间点 \(P_i\) 存在一定的噪声,所以对所有的匹配点,式 3.3.1 不一定恒等,即始终存在一个误差,这个误差称为重投影误差,光束法平差目标为最小化所有匹配的重投影误差和,从而获得位姿和估计点最优估计。光束法平差的非线性最小二乘表达如下: \[ \hat T,\hat P_i = \arg \min_{T,P_i} \frac{1}{2}\sum_{i=1}^n \vert\vert \pmb u_i - \frac{1}{s_i} KTP_i \vert \vert_2^2 \tag{3.3.2} \]
定义单个点误差为: \[ e = \pmb u - \frac{1}{s}KTP \tag{3.3.3} \] 根据 3.1 节的非线性优化模型,需要得到我们需要得到误差对优化变量 K、P 的雅可比矩阵,以更新迭代待优化变量。
定义变量 \(P'\) 满足: \[ \begin{align} P' = (TP)_{1:3} &= \left[ \begin{matrix} X' & Y' & Z' \end{matrix}\ \right]^T \tag{3.3.4}\\ e &= \pmb u - \pmb u' \tag{3.3.5} \\ \pmb u' &= \frac{1}{Z'}KP' \tag{3.3.6} \end{align} \] 根据链式求导法则,可得 \(e\) 关于 \(P\) 的雅可比矩阵为: \[ \begin{align} J_P(P) = \frac{\partial e}{\partial P'} \frac{\partial P'}{\partial P} \tag{3.3.7} \end{align} \] 相机内参矩阵定义为: \[ K = \left[ \begin{matrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{matrix} \right] \tag{3.3.8} \] 式 3.3.8 带入式 3.3.6 可得: \[ \begin{align} \pmb u' &= [u'\quad v']^T\\ u' = f_x \frac{X'}{Z'} + c_x &,\quad v' = f_y\frac{Y'}{Z'} + c_y \tag{3.3.9}\\ \end{align} \] 由式 3.3.7、3.3.8、3.3.9 可得: \[ \frac{\partial e}{\partial P'} = - \left[ \begin{matrix} \frac{\partial u'}{\partial X'} & \frac{\partial u'}{\partial Y'} & \frac{\partial u'}{\partial Z'} \\ \frac{\partial v'}{\partial X'} & \frac{\partial v'}{\partial Y'} & \frac{\partial v'}{\partial Z'} \\ \end{matrix} \right] = - \left[ \begin{matrix} \frac{f_x}{Z'} & 0 & -\frac{f_xX'}{Z'^2} \\ 0 & \frac{f_y}{Z'} & \frac{f_yY'}{Z'^2} \end{matrix} \right] \tag{3.3.10} \] 由式 3.3.4 可得 \(P'\) 对于 \(P\) 的导数为: \[ \begin{align} P' &= RP + t \\ \frac{\partial P'}{\partial P} &= R \tag{3.3.11} \end{align} \] 式 3.3.10、3.3.11 带入式 3.3.7 可得误差关于空间点的雅可比矩阵为: \[ J_P(P) = - \left[ \begin{matrix} \frac{f_x}{Z'} & 0 & -\frac{f_xX'}{Z'^2} \\ 0 & \frac{f_y}{Z'} & \frac{f_yY'}{Z'^2} \end{matrix} \right] R \tag{3.3.12} \] 由 3.2 节可以得到误差对位姿变化的导数,这里相机位姿使用李代数 \(\xi\) 表示,位姿上的扰动为 \(\delta \xi\)。从式 3.2.9、3.3.4、3.3.10 可得: \[ \begin{align} J_T(\delta\xi) &= \frac{\partial e}{\partial P'}\frac{\partial P'}{\partial \delta\xi}\\ &= - \left[ \begin{matrix} \frac{f_x}{Z'} & 0 & -\frac{f_xX'}{Z'^2} \\ 0 & \frac{f_y}{Z'} & \frac{f_yY'}{Z'^2} \end{matrix} \right] \left[ \begin{matrix} \pmb I & -P'^{\wedge} \end{matrix} \right] \tag{3.3.13} \end{align} \] 由式 3.3.12,3.3.13 可以得到误差对位姿以及空间点的导数,便可以使用高斯牛顿法或者 LM 法迭代更新,位姿更新采用式 3.2.10。
3.4 初值构建
如 3.1 节所述,非线性最小二乘优化的结果不一定是全局最优,所以需要构建良好的初值。对于光束法平差,可以使用 EPNP 等算法快速构建相机位姿的初值,然后使用迭代优化。目标三维点云可由三角测量得到,并作为点云初始值。
四、实验结果
4.1 理论验证
此部分代码以提交至本人 Github:https://github.com/Weijun-Lin/SLAM-Try/tree/master/BA-ceres
利用生成的数据进行理论验证,使用一个相机的 3D-2D 匹配优化位姿以及点云。步骤如下:
- 构建实验数据,确定相机内参矩阵以及相机真实位姿,并生成点云,根据相机成像模型建立 3D-2D 匹配,相机位姿使用李代数 \({\frak se}(3)\) 表示,前三维为平移,后三维为旋转即 \({\frak so}(3)\)
- 对真实位姿以及 3D 点云添加噪声干扰,得到待优化数据
- 使用光束法平差(BA)优化
- 利用均方误差(MSE)作为评价标准
原始位姿如下:
- 相机内参:\(3\times 3\) 的单位阵
- 相机真实位姿:\([0 \quad 0 \quad -20 \quad 0\quad 0 \quad 0]\)
- 添加噪声后位姿:\([3.6e^{-2} \quad -8.4e^{-2} \quad -19.99 \quad 2.8e^{-3}\quad -1.89e^{-3} \quad -8.87e^{-4}]\)
原始点云图:
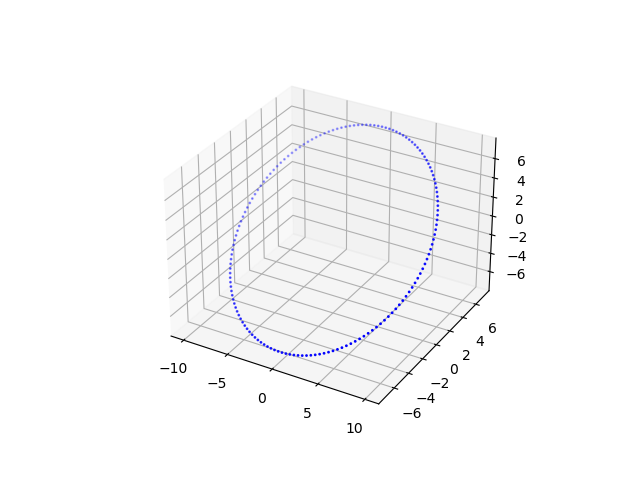
光束法平差优化后位姿为: \[ [3.55e^{-2} \quad -7.31e^{-2} \quad -20.036 \quad 1.92e^{-3} \quad -1.56e^{-3} \quad 1.3e^{-4}] \] 噪声干扰后点云以及光束法平差优化后点云如下图:
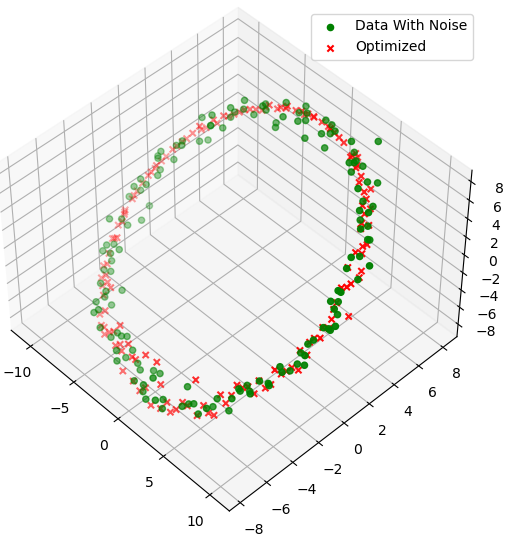
均方误差统计如下表:
| 位姿误差 | 点云误差 | |
|---|---|---|
| 优化前 | 0.091614 | 0.78033 |
| 优化后 | 0.088821 | 0.59205 |
可以看出,位姿以及点云在光束法平差后得到了优化。
4.2 BAL 数据集测试
BAL 数据集地址:https://grail.cs.washington.edu/projects/bal/,BAL 数据集包含了多幅图像,包含了 3D 空间点云,以及在每一副图像上的匹配点。这里使用的是 problem-16-22106-pre.txt.bz2 数据。此部分代码参考自 Github15,地址为:https://github.com/gaoxiang12/slambook2/tree/master/ch9。
优化之前点云图为:
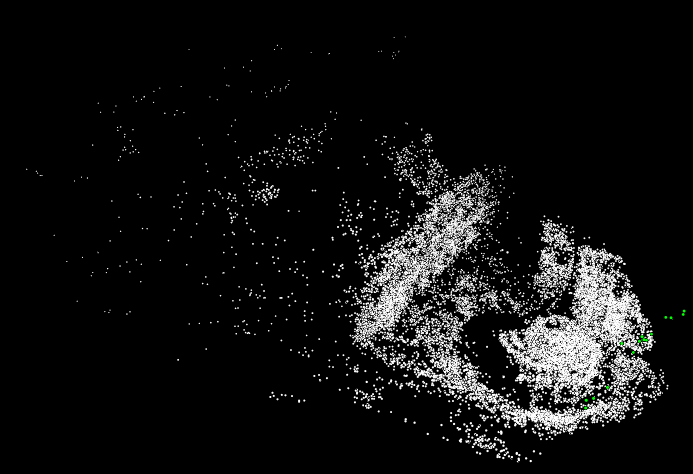
优化之后点云为:

可以看出优化之后点云将原常见轮廓更好的体现了出来
五、结论
综上,光束法平差对大规模点云优化以及相机位姿估计有很大的作用,但由于优化参数过于庞大,带来的空间以及时间开销都是巨大的。所以需要对问题规模做合理的约束。
光束法平差本质是一个非线性优化,它需要构建良好的初值,初值的确定对其优化效果特别重要。在 4.1 节,优化效果不是特别好,原因在于相机位姿只有一个,当存在多个相机位姿提供多个匹配关系时,优化效果会更加,如 4.2 节所示。