对极几何简单介绍
相机模型
《CV中的多视图几何》——再谈相机模型 - 知乎 (zhihu.com)
An Introduction to Epipolar Geometry | Sanyam Kapoor (perhapsbay.es)
小孔相机是相机模型的简化,小孔与成像平面之间的距离称为焦距。一般来说,小孔越小成像越清晰,但太小会造成衍射,导致成像模糊。
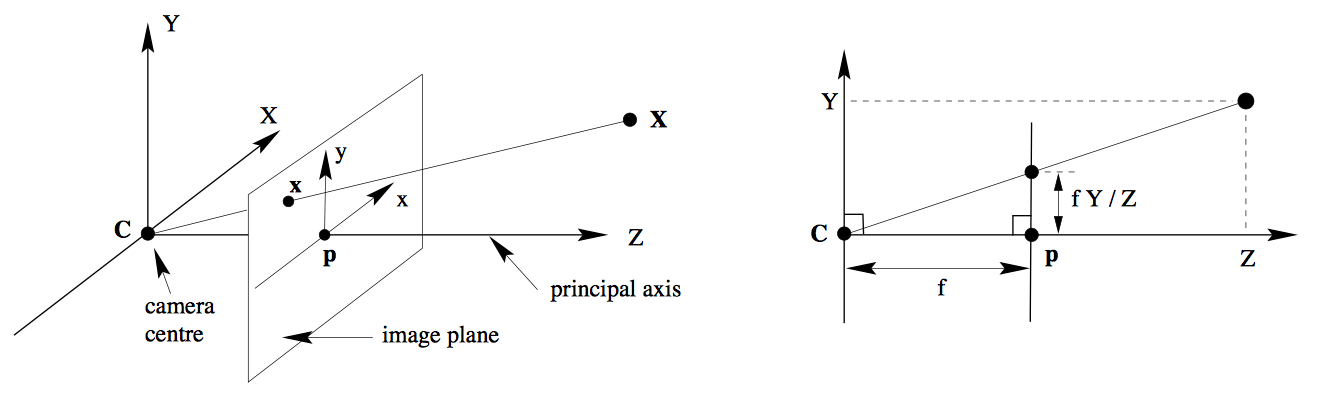
由相似三角形可得,空间上一点 \((X,Y,Z)\) 在成像平面上的点为:\((f\frac{X}{Z},f\frac{Y}{Z})\),矩阵表达如下: \[ \left( \begin{matrix} fX\\ fY\\ Z \end{matrix} \right) = \left[ \begin{matrix} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{matrix} \right] \left( \begin{matrix} X \\ Y \\ Z\\ 1 \end{matrix} \right) \tag{1} \] 即 \(\mathbf{x} = P\mathbf{X}\),需要注意的是,这里矩阵相乘的结果还需要除以第三个分量的 \(Z\) 才为真正的图像平面坐标(齐次化),即 \(\bf x\) 为摄像机坐标系下的坐标,除以第三个分量为图像坐标系下的点,即像素点,其中矩阵: \[ K = \left[ \begin{matrix} f_x & s & p_x \\ 0 & f_y & p_y \\ 0 & 0 & 1 \end{matrix} \right] \] 为相机内参矩阵,为式(1)矩阵的拓展,其中 \(f_x,f_y\) 表示相机像素长宽不一定一致,\(p_x,p_y\) 为成像平移,因为不一定在中心,\(s\) 为仿射畸变,即成像横纵轴不一定垂直。理想状态下相机如式(1)所示。
令 \(\bf p\) 表示图像坐标系上的点有:\(Z\mathbf{p} = \mathbf{x} = K\mathbf{X}\),其中 \(X = (X,Y,Z)\),归一化坐标表示为 \(\mathbf{\hat X} = (X/Z, Y/Z, 1)\),也就是将坐标都压缩到 \(Z = 1\) 平面上。
归一化坐标和图像坐标有以下关系: \[ \begin{align} Z\mathbf{p} &= \mathbf{x} = K\mathbf{X} \\ \mathbf{p} &= K\mathbf{\hat X} \\ \mathbf{\hat X} &= K^{-1}\mathbf{p} \tag 2 \end{align} \]
对极几何 Epipolar Geometry
Introduction To Epipolar Geometry | by Nabil MADALI | Towards Data Science
An Introduction to Epipolar Geometry | Sanyam Kapoor (perhapsbay.es)
对极几何考虑的是两个成像视图中固有的投影几何,独立于场景结构,且只取决于相机的内外参数。一般用于解决双目匹配和视图对应点搜索一类的问题。
对极几何模型如下图所示:
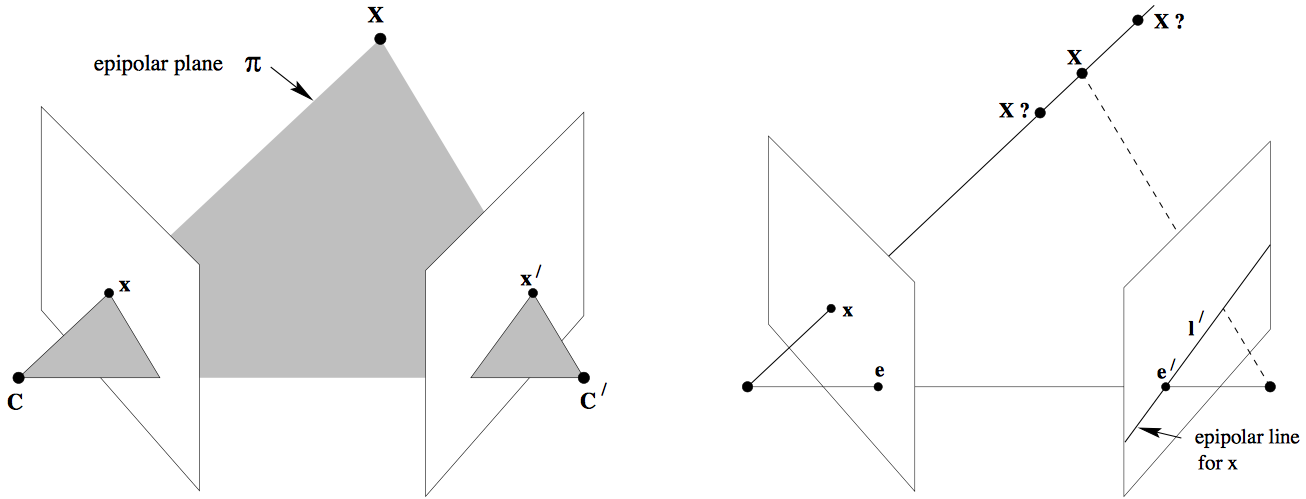
上图中 \(\bf{C,C'}\) 为两个摄像机的光心,\(\mathbf{X}\) 为三维空间中的目标点,它在两幅图像的投影点分别为 \(\bf{x},\bf{x'}\),光心连线交两个成像平面分别于 \(\bf{e}, \bf{e'}\)。对极几何的一些基础概念如下:
- 基线 Baseline:光心连线 \(\bf{CC'}\)
- 对极平面 Epipolar plane:由光心和目标点组成的平面 \(\bf{\pi:CXC'}\)
- 极点 Epipolar Point:光心连线交成像平面的点 \(\bf{e,e'}\)
- 极线 Epipolar line:投影点和极点的连线 \(\bf{l:xe,l':x'e'}\)
对极几何主要有以下两个方向的用途:
- 立体匹配问题。两个投影之间的空间位置关系已知的情况下,由于对极几何模型带来的一致性约束,将搜索空间定位在两张图像上,也就是在相应的极线上搜索。将最初的二维搜索问题直接简化为一维搜索。双目测距就是一个典型应用。
- 确定两个拍摄点的相对位置和姿态。在不知道视角位置的情况下,通过搜索图像对中的匹配点,便可以确定它们之间的相对位置和姿态。广泛应用于机器人导航,地图构建,三维重建等方向。
本质矩阵 Essential Matrix
《CV中的多视图几何》——基础矩阵、本质矩阵 - 知乎 (zhihu.com)
VSLAM 笔记——我们如何通过图像来计算位姿的变化:对极几何 - 知乎 (zhihu.com)
Introduction To Epipolar Geometry | by Nabil MADALI | Towards Data Science
两个相机 \(\bf {C,C'}\) ,对应的相机若以 \(\bf C\) 为标准,有以下式子成立: \[ \begin{align} Z_1p_1 &= K_1X \\ Z_2p_2 &= K_2X' \\ &= K_2(RX+T) \\ &= K_2(Z_1RK_1^{-1}p_1 + T) \\ K_2^{-1}p_2 &= \frac{1}{Z_2}(Z_1RK_1^{-1}p_1 + T) \\ \text{由式(2)可得:}\\ x_2 &= \frac{1}{Z_2}(Z_1Rx_1 + T) \tag{3} \end{align} \] 式(3)的 \(x_1,x_2\) 为 \(X,X'\) 在各自坐标系下的归一化坐标,其中 \(R,T\) 分别为旋转矩阵和平移向量。式(3)两边同与 \(T\) 做叉积可得: \[ T\times x_2 = \frac{Z_1}{Z_2}T\times R x_1 \] 然后与 \(x_2\) 做点积可得: \[ x_2\cdot(T\times x_2) = x_2\cdot (\frac{Z_1}{Z_2}T\times R x_1) = 0 \tag 4 \] 对于向量 \(a = (a_1,a_2,a_3)\) ,向量 \(b = (b_1,b_2,b_3)\) 有以下关系成立(可参考反对称矩阵 (Skew-symmetric Matrix) - 技术刘 (liuxiao.org)): \[ \begin{align} a \times b &= [a]_{\times} b \\ [a]_{\times} &= \left[ \begin{matrix} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \\ \end{matrix} \right] \end{align} \]
所以式(4)可以化简为: \[ \begin{align} x_2 \cdot [T]_{\times} R x_1 &= 0 \\ x_2^T E x_1 &= 0 \tag 5 \end{align} \] 令 \(E = [T]_{\times}R\),即为本质矩阵,反映了归一化坐标与相机相对位置姿态的关系。
基础矩阵 Fundamental Matrix
An Introduction to Epipolar Geometry | Sanyam Kapoor (perhapsbay.es)
根据式(2)中归一化坐标与像素坐标的关系有: \[ x_1 = K_1^{-1} p_1 \\ x_2 = K_2^{-1}p_2 \] 带入式(5)可得: \[ \begin{align} p_2^TK_2^{-T}EK_1^{-1}p_1 &= 0\\ p_2^T F p_1 &= 0 \tag{6} \end{align} \] 令 \(F = K_2^{-T}EK_1^{-1}\),其中 \(F\) 就称为基础矩阵,基础矩阵表示了像素坐标与摄像机内参以及相机相对位置姿态之间的关系。
基础矩阵本质上是点到极线的一个映射。此映射推导过程如下:
\(y_1 = P_1X\),由 \(y_1\) 可确定一条直线,这条直线均可投影到 \(y_1\) 处,如下: \[ X(\lambda) = P_1^+ y_1+\lambda C_1 \] \(y_1,X(\lambda)\) 分别为 \(C_1\) 下的图像坐标,\(C_1\) 坐标系三维坐标。\(P_1^+\) 为 \(P_1\) 的伪逆,有 \(P_1^+ = P_1^T(P_1P_1^T)^{-1}\),可验证 \(P_1 X(\lambda) = P_1P_1^+y_1 + \lambda P_1 C_1 = y_1\)。(伪逆可参考:线性代数笔记34——左右逆和伪逆 - 我是8位的 - 博客园 (cnblogs.com))
\(X(\lambda)\) 通过另外一个相机投影矩阵 \(P_2\) 投影便可以获得极线 \(l'\),可以取 \(X(\lambda)\) 上两个特殊点 \(P_1^+y_1,C_1\) ,分别通过 \(P_2\) 投影可得 \(P_2P_1^+y_1,P_2C_1\),注意这里的 \(P_2\) 包括了外参矩阵和内参矩阵。这两个点叉乘便可以得到极线 \(l'\) 的参数表达式,\(P_2C_1\) 就是极点 \(e'\) 所以有: \[ l' = e' \times P_2P_1^+y_1 = [e']_{\times}P_2P_1^+y_1 \tag 7 \] \(X\) 在 \(C_2\) 下的投影点为 \(y_2\),显然 \(y_2\) 在极线上,所以有: \[ y_2\cdot l' = y_2^T [e']_{\times}P_2P_1^+y_1 = 0 \] 令 \(F = [e']_{\times}P_2P_1^+\) 便得到: \[ y_2^T F y_1 = 0 \]
此时这里的 \(y_1,y_2\) 为相机坐标系下的点,和对于图像坐标系的点有以下关系 \(y_1 = Z_1p_1,y_2 = Z_2p_2\),带入上式消去常数 \(Z_1,Z_2\),可得式(6): \[ p_2^T F p_1 = 0 \] 极线还可表达为:\(l'=e'\times y_2\),根据单应矩阵的性质,可得 \(y_2 = H_{\pi} y_1\),即有 \(l' = e' \times H_{\pi} y_1\),对比式(7) ,可以得到: \[ H_\pi = P_2P_1^+ \] 此时便得到了基础矩阵,相机矩阵,单应矩阵之间的联系。
之前提到 \(P_2\) 由相机内参和外参组成,可令 \(C_1\) 相机坐标系和世界坐标系重合,代数表达如下: \[ P_1 = K_1[\mathbf{I}|\mathbf{0}] \\ P_2 = K_2[\mathbf{R}|\mathbf{T}] \\ \] 《CV中的多视图几何》——基础矩阵、本质矩阵 - 知乎 (zhihu.com)中解释了如何将 \(F = [e']_{\times}P_2P_1^+\) 推导为 \(F = K_2^{-T}EK_1^{-1}\) 的过程。
补充
以上引用文章中的推导将归一化坐标,图像坐标,摄像机坐标描述的很模糊,摄像机坐标到图像坐标本质上是一个齐次化过程,但都描述的比较模糊。
一些另外补充:
如何得到本质矩阵 \(E\) 以及如何将本质矩阵 \(E = [T]_{\times}R\) 经过SVD 分解得到 \(T,R\) 的方法参考:VSLAM 笔记——我们如何通过图像来计算位姿的变化:对极几何 - 知乎 (zhihu.com),一般通过图像匹配点获得基础矩阵,然后得到本质矩阵,最后分解得到 \(R,T\),相机内参矩阵可通过标定得到。