三维重建算法综述-张彦雯小结

发表于 2021-06-03 分类于 Computer Science ， CV&CG&DIP ， CV ，三维视觉与SLAM 阅读次数：本文字数： 1.4k 阅读时长 ≈ 5 分钟

关键词：三维重建；图像；稀疏点云重建（SFM）；稠密点云重建（MVS）；评价指标

下载链接

获取三维模型主要通过以下三种方式：

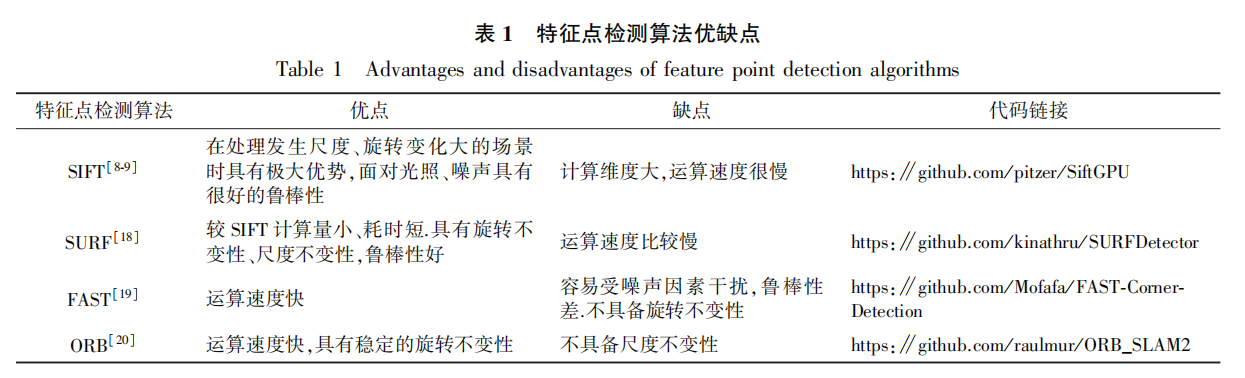
文章主要介绍基于多幅图像的三维重建算法，主要包括稀疏点云重建（Structure From Motion，SFM）；稠密点云重建（Multi-View System，MVS）。其中 SFM 包括特征点检测与匹配（SIFT，SURF，FAST等）以及 SFM 重构两个部分。

SFM 重构大致分为三类：增量式重构、全局式重构、混合式重构。在 MVS 中，深度图的计算尤为重要。

稀疏点云重建 SFM

SFM 通过相机的移动确定目标的空间和几何关系，特征点匹配后运用 SFM 重构算法，恢复出相机的参数，相机之间的相对位置关系以及场景的稀疏点云，最后捆绑调整优化相机位姿、相机参数、场景结构。

流程总结为：特征点检测、匹配，相机位姿（旋转矩阵 R，平移矩阵 T）初始值的求解，捆绑调整优化相机位姿、相机参数、场景结构。

SFM 重构为利用相机运动轨迹来估算相机参数，初步匹配生成的的特征点比较粗糙，所以常用几何约束删除匹配错误的特征点对。SFM 重构主要有增量式和全局式。

增量式重构是从两张图像中恢复相机的旋转矩阵 R 和平移矩阵 T，然后添加图像，利用PnP 计算出第三幅图像的 R、T，通过三角化重建出更多的场景。噪声的干扰会造成结果漂移，所以需要使用 BA（Bundle Adjustment，光束法平差）。每次添加图像完成三角化后都需要进行优化。

步骤为：初始化、PnP 解算，三角化，BA 算法优化。重要的步骤为 PnP 求解相机位姿，主要有 P3P，EPnP，DLT，UPnP，MRE。

PnP：已知 n 个三维空间点坐标（相对于某个指定的坐标系A）及其二维投影位置的情况下，如何估计相机的位姿（即相机在坐标系A下的姿态）

增量式在对大规模场景重建时由于误差累积会造成场景漂移以及反复地捆绑调整花费大量时间。

全局式重构采用的是将相机相对位姿均匀分布的方法，该方法在处理大规模重建时，相机之间的相关性不同，会导致重建效果差。

混合式重构就是把前两者进行融合。

SFM 重建比较稀疏，需要 MVS 进行完善，MVS 的目的是通过最佳方法对不同图像上的同一个点进行匹配，增强重建场景的稠密性。MVS 的主要任务是通过一种最佳搜索的方法，匹配不同图像上的同一个点。也就是在极线上进行探测，寻找两张图片上的同一点，主要方法为逐像素判断，由此提出了一致性度量函数。

深度图是指将相机到场景中各点距离作为像素值的图像，是 MVS 的一大重点。主要方法如下：

分为有真实模型和无真实模型两类。

无真实模型的评价是通过对比输入数据与重建之后的数据一致性程度来实施的，其方法有重建误差法，积分误差法。

有真实模型的评价通过重建之后的模型与真实模型进行对比来实施，主要有形状误差法，分解法，相位矩不变量法，多指标评价法等。

这些算法都有缺陷：

基于图像的三维重建不需要精密的测量一起，成本低，同时该方法计算出了相机的内外参数，使得重建效果更为精确，具有快速、简便、逼真的优点，能较好地实现现实事物的虚拟化，但仍然存在一些缺点：