单应变换的局限性

单应变换

单应变换就是两个平面内保持共线的变换，变换是一个 3*3 的矩阵，因为齐次坐标的尺度无关性所以只有8个自由度。DLT（直接线性变换）算法讨论了单应变换的相关性质，以及变换矩阵的求解。

局限性

单应变换简单来说就是可以将一个四边形映射为另一个任意的四边形，只需要满足共线点变换后仍为共线即可。在很多算法中都使用到单应变换，但单应变换只能模拟两种情况的变换：

1. 相机几何中心位置不变，目标场景任意
2. 相机位置任意，目标场景为平面（或近似为平面，很多低空遥感图像都视作为平面）

在论文 Perspective-SIFT: An efficient tool for low-altitude remote sensing image registration 中提取的透视不变特征使用的就是单应变换模拟。

但上面两个局限性使得在相机位置改变（平移变换）时，场景需要约束到平面。

局限性的解释

下面的内容参考自 Homography | 奇点视觉 (singvision.net)

相机位置改变的图示如下：

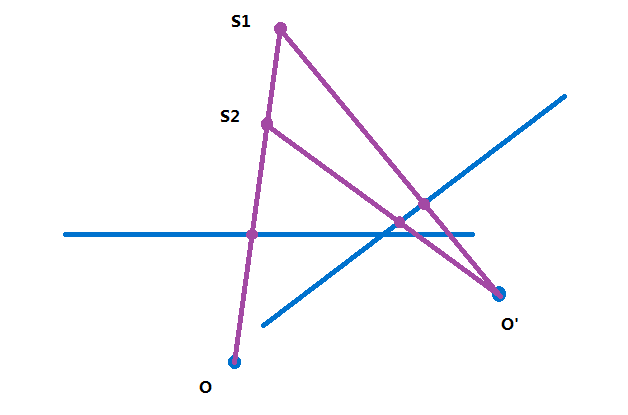
其中 \(o,o'\) 表示相机位置，横线表示相机的成像平面，\(s_1,s_2\) 表示目标物，这里的 \(s_1,s_2\) 在 \(o\) 的视角下就成为了一个点，也就是说存在遮挡，这样使用单应变换就不能将一幅图像变换为另一幅图像，在图像拼接中，也就找不到对应点。

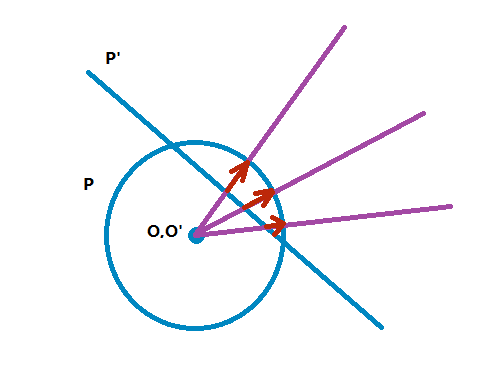
但是当目标为平面时，无论视角怎么改变都不会丢失点（除非视角在平面上），当视角位置不变，仅存在旋转角度的改变时，此时单应也能模拟这种变换。

视角不变时，单应可以模拟变换，但会造成另一种情况：

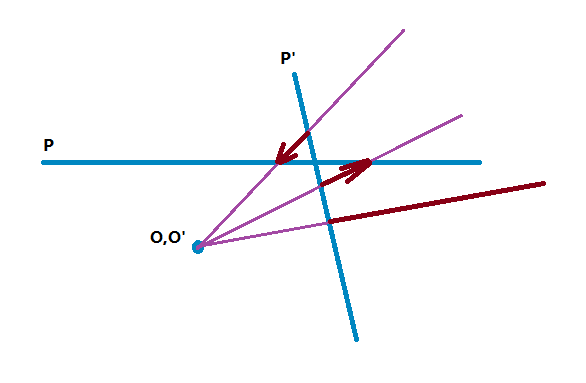
成像在 \(P'\) 上为均匀的点，但在 \(P\) 上却是间隔非均匀的点，当 \(P\) 和 \(P’\) 垂直时，这种差距更大，可能会使得 \(P’\) 上的点在 \(P\) 上变成无穷远的点，这在大视角的图像拼接会造成很大的误差。一种解决方法是将图像重投影到均匀圆柱面或者球面上：