MLS移动最小二乘法原理及其实现
原理介绍
原理可参考基于移动最小二乘法的曲线曲面拟合,曾清红,卢德唐,这里面已经讲得很详细了。可以结合CSDN 移动最小二乘原理,一起看,曾清红论文的式子稍微有点难懂,结合起来看很不错。
MLS(Moving Least-Squares),移动最小二乘,是一种比较方便的曲线、曲面拟合方法,和传统最小二乘法相比有很多优点,在论文中都提到了。这里主要对其原理做个简单的说明和补充。
最小二乘法是通过给定的目标函数和点集中找到目标函数的一组系数使其误差最小(L2范式)。一般是多项式函数,未知数为系数,通过找到最佳的系数来拟合。这就有很大的缺陷,对于一般的函数,很难用一个多项式函数来全局拟合。但分段拟合,其中的光滑又很难保证,会带来很大的困难。
拟合函数的建立
移动最小二乘法其实本质上也类似,不同的是它采取的系数是 x 的函数,也就是对不同的目标拟合点它所属的多项式函数是不同的。这就有了很大的灵活性。有点上面直接分段的意思。
在拟合区域的一个局部上,拟合函数 \(f(x)\) 表示为: \[ f(x) = \sum_{i=1}^m \alpha_i(x) p_i(x) = p^T(x)\alpha(x) \] 乘积相加就可以转换为向量点积,其中: \[ \begin{align} \alpha(x) &= [\alpha_1(x),\alpha_2(x),\cdots,\alpha_m(x)]^T \\ p(x) &= [p_1(x), p_2(x),\cdots,p_m(x)]^T \end{align} \] \(\alpha(x)\) 为待求系数,每一个元素都是 x 的函数。\(p(x)\) 为基函数,一个多项式函数的基,例如拟合线可以使用 \([1,x]^T, [1,x,x^2]\) 这类的,对于二维问题(拟合曲面)则可以采用 \([1,x,y]^T,[1,x,y,x^2,xy,y^2]\),优化的目标函数为: \[ J = \sum_{i=1}^n w(x-x_i)[f(x_i)-y_i]^2 = \sum_{i=1}^n w(x-x_i)[p^T(x_i)\alpha(x)-y_i]^2 \rightarrow \mathrm{min} \] 表示的意思其实是对某个小区间,其中的 x 和它对应的 \(\alpha(x)\) 使得上式最小,这里把 x 视作为已知量,要求的未知量是向量 \(\alpha(x)\)。上面的 \(f(x)\) 我修改为 \(f(x_i)\) ,感觉这才符合论文意思。因为 \(w(x-x_i)\) 为权函数,并且具有紧支性(范围之外为 0)也就是只考虑与 “x” 这个小区间相邻的部分,其余那些远离它的部分没有影响。
其中 n 为已知点的数量,\(x_i,y_i\) 为已知点集的点。对拟合量 x 来说,未知的只有 \(\alpha(x)\) 所以对它求导可得: \[ \begin{align} \frac{\partial J}{\partial \alpha} &= A(x)\alpha(x) - B(x)y = 0\\ A(x) &= \sum_{i=1}^n w(x-x_i)p(x_i)p^T(xi) \\ B(x) &= [w(x-x_1)p(x_1), w(x-x_2)p(x_2), \cdots, w(x-x_n)p(x_n)] \\ y^T &= [y_1, y_2, \cdots,y_n] \end{align} \] 可以先对 \(\alpha_i(x)\) 求导,然后拓展到向量形式,偏导等于 0 时取到最小值,此时有: \[ \alpha(x) = A^{-1}(x)B(x)y \] 此时便得到 x 对应的系数向量,其中 \(A^{-1}(x),B(x),y\) 为 \(m\times m,m\times n,n\times 1\) 的矩阵,把 \(\alpha(x)\) 带入 \(f(x)\) 定义式有: \[ f(x) = p^T(x)A^{-1}(x)B(x)y = \Phi(x) y \] \(\Phi(x)\) 就称为形函数,是一个 \(1\times m\) 的向量
权函数
权函数在最小移动二乘法有很大的作用,甚至是核心作用。它具有紧支性,也就是权函数在 x 的一个子域内不等于
零 在这个子域之外全为零,这个子域称为支持域。权函数是非负的,并且随着距离(\(\vert\vert x-x_i \vert\vert\)) 的增加而减小,也就是原理 x 的认为对 x 的影响小。权函数还需要具有一定的光滑性,因为需要继承原函数的连续性。论文给出的是三次样条函数曲线(这里归一化了): \[ w(\overline s) = \left \{ \begin{align} & \frac{2}{3}-4 \overline s^2 + 4\overline s^3 & &(\overline s \le \frac{1}{2}) \\ & \frac{4}{3}-4\overline s+4\overline s^2-\frac{4}{3}\overline s^3 & &(\frac{1}{2} <\overline s\le 1 ) \\ & 0 &&(\overline s > 1) \end{align} \right. \]
其中,\(s = x - x_i,\overline s = \frac{s}{s_{max}}\),\(s_{max}\) 为影响区域的大小,也就是支持域的大小。需要注意的是,支持域的选取很麻烦,因为拟合函数需要矩阵 A 的逆,这就需要保证每个拟合点的支持域中的非共线(共面)的点数达到最低要求。对于使用一维二次基 \([1,x,x^2]\) 的曲线拟合,就需要保证拟合点 x 支持域中至少有三个非共线的点。权函数并不是只可以用这个,只要满足上述的特征就可以。
可以考虑支持域的动态化,唯一的支持域对非均匀分部的曲线拟合很不友好,动态化或许可以缓解。
Matlab 实现
这里使用 matlab 实现,代码不多,只要把思路理清即可,这里分为曲线和曲面拟合,分别对应论文中的两个实验,使用的也是论文中的数据。
曲线拟合
虽然使用和论文相同的数据,但这里采用了一维二次基 \([1,x,x^2]\) 拟合,可以看出比论文的效果稍微好一些。
代码如下:
1 | clc;clear; |
拟合图如下:
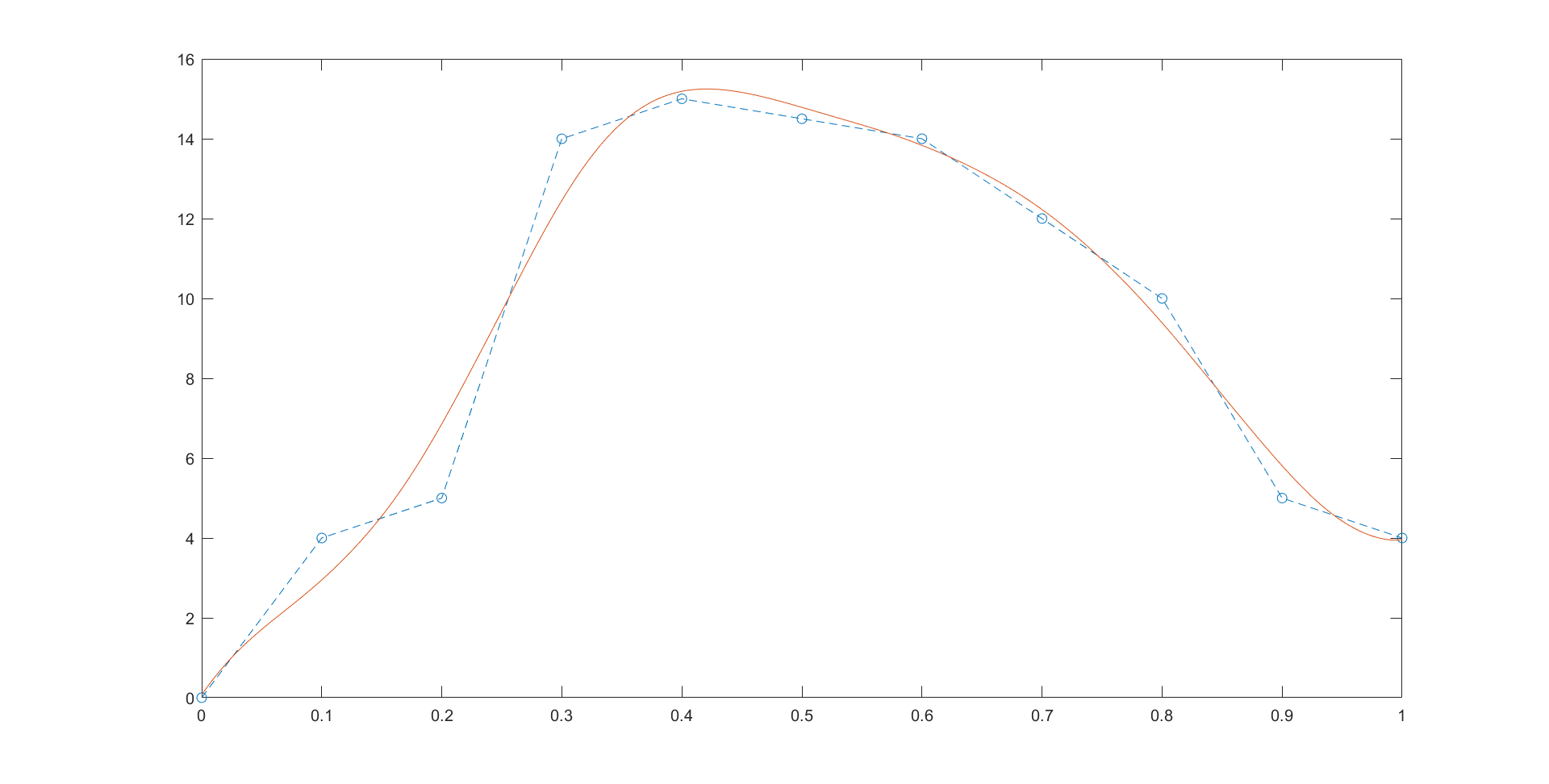
圆点为数据,虚线为直接连接的线,曲线为拟合线
曲面拟合
曲面使用的是论文给的函数,使用的和论文的一样的二维线性基 \([1,x,y]\) \[ \begin{align} z &= f(x,y) \\ &= 2*(1-x)^2 * exp(-x^2 - (y+1)^2) - 10*(x^4/5 - y^5) * exp(-x^2 - y^2) - 1/3*exp(-(x+1)^2 - y^2) \end{align} \] 函数图像为:
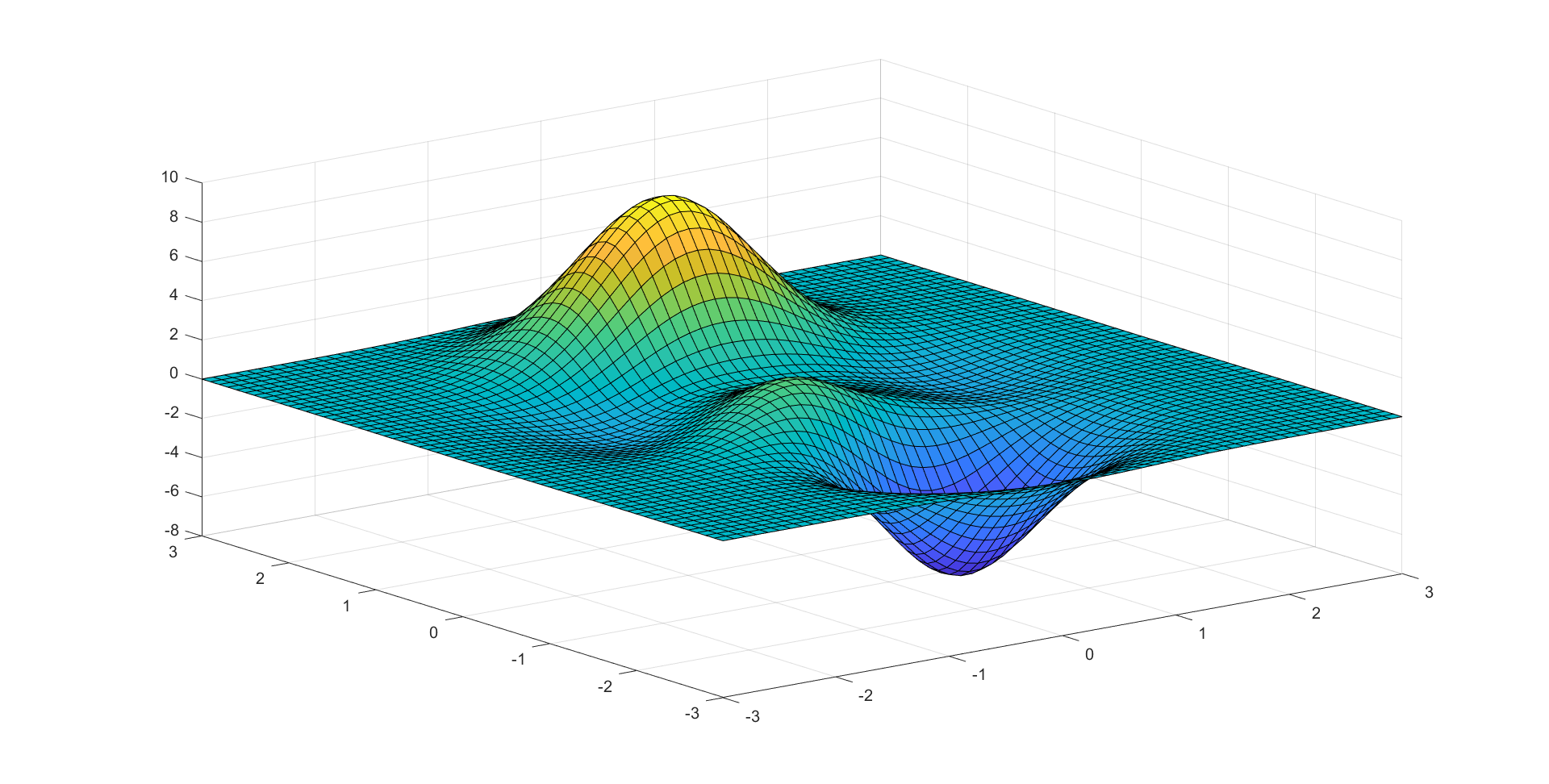
代码如下:
1 | clc;clear; |
拟合图如下:
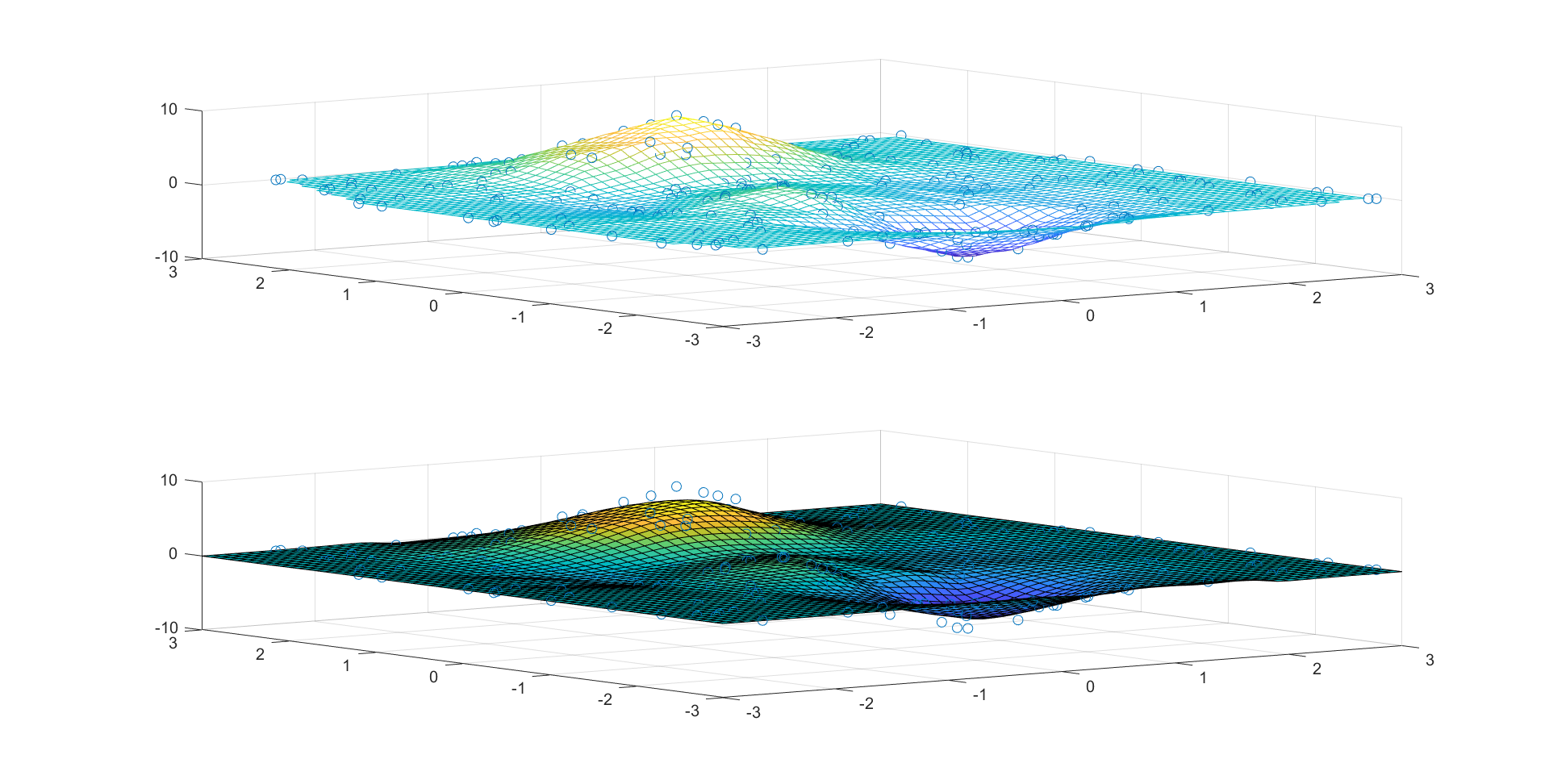
上面为随机生成的点图和 matlab 插值生成的网格图,下面为 MLS 拟合的曲面,效果还是不错的