霍夫变换直线检测原理实现

发表于 分类于 ， ， 阅读次数： 本文字数： 795 阅读时长 ≈ 3 分钟

简单介绍

霍夫变换可以用于边缘检测，更一般的则可以拟合曲线。基本原理如下：由曲线的定义式可得，如果 XY 确定，其对应的未知数构成的等式也可视作一个曲线表达式，这个新的表达式称作参数空间（自变量为原来的参数）改变 XY 的过程中这些位置构成的新的表达式必会都经过某一个固定点，这个固定点代表的参数就是原来曲线表达式。

但实际上的曲线会受到噪声影响，也就是说参数空间中所有的表达式并不会经过同一点，而是大部分曲线会经过某一固定点，这个固定点可能不止一个，所以我们将参数空间切分为一个个子区域，并统计子区域中线的交点（也可以直接统计线的点数，只要代表密度即可），交点最多的那个区域就是原曲线的参数。

更加详细的介绍可见《数字图像处理》中文第三版 P472 10.2.7 边缘检测和边界检测。或参考Matlab 霍夫变换 ( Hough Transform） 直线检测 - Pony_s - 博客园 (cnblogs.com)

代码实现

以下为 matlab 代码实现，基本实现过程如下：

  1. 实现生成直线
  2. 给直线增加噪声
  3. 对噪声处理后的图像生成其参数空间
  4. 对参数空间的所有曲线做直方图统计，得到最大数量的参数表达
  5. 获得拟合的直线

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
% 霍夫变换 & 直线
% 生成直线 y = 2x + 3
x = -5:5;
y = 2*x + 3;
% 添加噪声
y_noise = y + randn(1, size(x, 2))*1.5;
figure("name", "霍夫变换");
subplot(2,2,3);
% 绘制原始线和噪声后的线
plot(x,y, x, y_noise, '--+');
title("直线拟合");
axis equal
grid on

% 绘制霍夫变换参数空间，ysin(theta)+xcos(theta) = p
% 设置范围
subplot(2,2,[1,2]);
hold on
% 设置角度范围
[theta_min, theta_max] = deal(0, 2*pi);
theta = theta_min:0.1:theta_max;
% 预开辟所有点的参数空间存储
p_all = zeros(size(x,2), length(theta(:)));
for i = 1:size(x, 2)
    % 生成对应范围内的参数曲线
    p = y_noise(i) * sin(theta) + x(i) * cos(theta);
    p_all(i, :) = p;
    % 绘制参数空间的曲线
    plot(theta, p);
end
title("参数空间");
hold off
axis normal
grid on
subplot(2,2,4)
% 统计其中每个子区域中的点数，并记录最大的
% 这里使用直方图hist3计算
theta_repeat = repmat(theta, 11, 1);
hist3([theta_repeat(:) p_all(:)], 'CDataMode','auto','FaceColor','interp');
title("直方图统计交点最多的区域");
% num 是每个bin的数量，center为对应的x,y坐标
[num, center] = hist3([theta_repeat(:) p_all(:)]);
% 找到最大的那个bin的下标并获取对应的参数
[i, j] = find(num == max(max(num)));
theta_best = center{1}(i);
p_best = center{2}(j);
% 获得拟合后的直线并绘制
y_simulate = (p_best - x*cos(theta_best))/sin(theta_best);
subplot(2,2,3);
hold on
plot(x, y_simulate);
legend(["y=2x+3", "y=2x+3+noise", "simulate"], 'Location', 'northwest');
hold off

最后的效果如下：

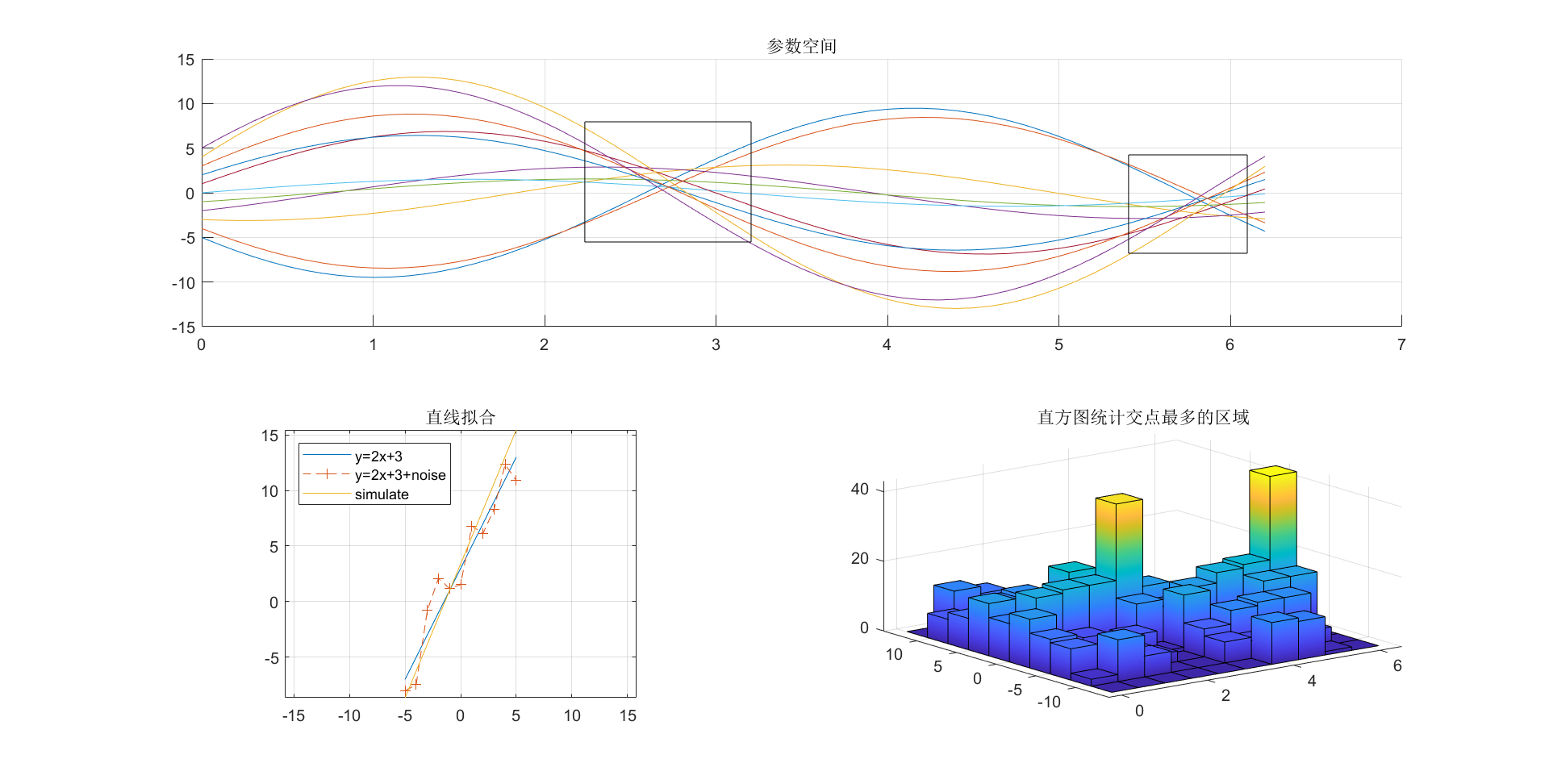
其中参数空间的方框为交点比较多的，也就是比较密集的，这里有两个，代码里就取了一个，另外一个也是可以的。