图像旋转算法实现 Python

发表于 分类于 ， ， 阅读次数： 本文字数： 1.4k 阅读时长 ≈ 5 分钟

旋转原理

参考博客：https://blog.csdn.net/liyuan02/article/details/6750828

如下图，推导点\((x_0,y_0)\)旋转\(\theta\)到到点\((x,y)\)，半径为R

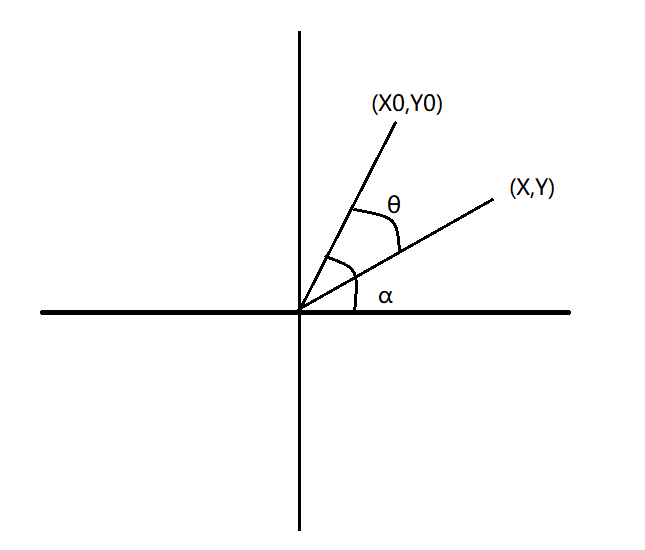
对于两点坐标可以这样表示：

\[ \begin{align} x_0 =& R*\cos\alpha \\ y_0 =& R*\sin\alpha \\ For:x\\ x =& R*\cos(\alpha-\theta) \\ =& R*(\cos\alpha\cos\theta+\sin\alpha\sin\theta) \\ =& x_0\cos\theta+y_0\sin\theta \\ For:y\\ y =& R*(\sin(\alpha-\theta)) \\ =& R*(\sin\alpha\cos\theta-\cos\alpha\sin\theta) \\ =& y_0\cos\theta-x_0\sin\theta \end{align} \]

使用矩阵表示有：

\[ \left[ \begin{matrix} x & y & 1 \end{matrix} \right]= \left[ \begin{matrix} x_0 & y_0 & 1 \end{matrix} \right] * \left[ \begin{matrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{matrix} \right] \]

此为顺时针旋转\(\theta\) ，逆时针旋转\(\theta\)只需要将 \(\theta=-\theta\) 即可，易得：\((x,y)\rightarrow(x_0,y_0)\)

\[ \left[ \begin{matrix} x_0 & y_0 & 1 \end{matrix} \right]= \left[ \begin{matrix} x & y & 1 \end{matrix} \right] * \left[ \begin{matrix} \cos\theta & \sin\theta & 0 \\ -\sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{matrix} \right] \]

用于实际的旋转矩阵

上一部分的旋转矩阵是以数字坐标系推导的，而图像坐标系是以左上角为原点的图像坐标系，我们需要将图像坐标系转换为数字坐标系，方便的也需要从数字坐标系到图像坐标系的逆转换

假设原图片大小为\(W,H\)，旋转后所包含图片的最小矩形大小为\(W^{'},H^{'}\)

设数字坐标系点为\((x,y)\)其相应的图像坐标系点为 \((x_0,y_0)\) 有如下表达式：

\[ \left[ \begin{matrix} x & y & 1 \end{matrix} \right]= \left[ \begin{matrix} x_0 & y_0 & 1 \end{matrix} \right] * \left[ \begin{matrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ -0.5W & 0.5H & 1 \end{matrix} \right] \]

\[ \left[ \begin{matrix} x_0 & y_0 & 1 \end{matrix} \right]= \left[ \begin{matrix} x & y & 1 \end{matrix} \right] * \left[ \begin{matrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0.5W^{'} & 0.5H^{'} & 1 \end{matrix} \right] \]

假设在图像坐标系中有点\((x_0,y_0)\)顺时针旋转\(\theta\) 到\((x,y)\)处转换后大小为\(W^{'},H^{'}\)，转换公式有：

\[ \left[ \begin{matrix} x & y & 1 \end{matrix} \right]= \left[ \begin{matrix} x_0 & y_0 & 1 \end{matrix} \right] * \left[ \begin{matrix} 1 & 0 & 0 \\ 0 & -1 &0 \\ -0.5W & 0.5H & 0 \\ \end{matrix} \right] * \left[ \begin{matrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{matrix} \right] * \left[ \begin{matrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0.5W^{'} & 0.5H^{'} & 1 \end{matrix} \right]\tag{1} \]

\[ \left[ \begin{matrix} x_0 & y_0 & 1 \end{matrix} \right]= \left[ \begin{matrix} x & y & 1 \end{matrix} \right] * \left[ \begin{matrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ -0.5W^{'} & 0.5H^{'} & 1 \end{matrix} \right] * \left[ \begin{matrix} \cos\theta & \sin\theta & 0 \\ -\sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{matrix} \right] * \left[ \begin{matrix} 1 & 0 & 0 \\ 0 & -1 &0 \\ 0.5W & 0.5H & 0 \\ \end{matrix} \right]\tag{2} \]

(1)式为前向映射（直接从原图映射到旋转后的图），（2）式为后向映射（用于旋转后映射到旋转前）

为什么需要后向映射而不是前向映射

之所以有后向映射是因为在前向映射中获取的旋转后坐标是浮点数，但是像素只能是整数，所以就产生了像素缺失

而从后向前映射像素信息都是存在的，但又存在映射到原图中的浮点坐标改如何选择颜色信息的问题

这就有内插值的问题，提供的解决办法有三个，最邻近内插、双线性内插、双三次内插，最邻近就是直接对浮点坐标取整，取最接近它的像素值，双线性内插就是取与它相邻的4个点，求线性渲染值

其本质就是：假设在数轴上有两个点A，B（A<B) AB中间有个点X，那么双线性内插就和知道X到点A的距离求X的值是一个道理，不过双线性需要对X和Y两个方向求值

双三次内插有点麻烦，这里。。我也不清楚，嘿嘿

可以参考https://blog.csdn.net/caomin1hao/article/details/81092134

Python 实践

所需外部库：

  • numpy（矩阵计算）
  • matplotlib (效果演示)
  • skimage （只读取使用其内置图片 换cv2读自己图片也可以）

使用按像素遍历，比较耗时

后向映射中使用最邻近内插和双线性内插（双三次内插暂未处理）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
import numpy as np
import matplotlib.pyplot as plt
import skimage.data
import skimage.io

angle = 30*np.pi/180
# 读取库图片 Attention 转换 默认为int8 运算时可能会溢出
img = skimage.data.chelsea().astype(int)
# 设置新的图像大小
h,w = img.shape[0],img.shape[1]
newW = int(w*abs(np.cos(angle)) + h*abs(np.sin(angle)))+1
newH = int(w*abs(np.sin(angle)) + h*abs(np.cos(angle)))+1
# Attention dtype
newimg1 = np.zeros((newH,newW,3),dtype = int)
newimg2 =  np.zeros((newH,newW,3),dtype = int)
newimg3 =  np.zeros((newH,newW,3),dtype = int)
# 设置旋转矩阵 scr -> dex
trans1 = np.array([[1,0,0],[0,-1,0],[-0.5*w,0.5*h,1]])
trans1 = trans1.dot(np.array([[np.cos(angle),-np.sin(angle),0],[np.sin(angle),np.cos(angle),0],[0,0,1]]))
trans1 = trans1.dot(np.array([[1,0,0],[0,-1,0],[0.5*newW,0.5*newH,1]]))
# des -> src
trans2 = np.array([[1,0,0],[0,-1,0],[-0.5*newW,0.5*newH,1]])
trans2 = trans2.dot(np.array([[np.cos(angle),np.sin(angle),0],[-np.sin(angle),np.cos(angle),0],[0,0,1]]))
trans2 = trans2.dot(np.array([[1,0,0],[0,-1,0],[0.5*w,0.5*h,1]]))
# 开始旋转
for x in range(w):
    for y in range(h):
        newPos = np.array([x,y,1]).dot(trans1)
        newimg1[int(newPos[1])][int(newPos[0])] = img[y][x]

for x in range(newW):
    for y in range(newH):
        srcPos = np.array([x,y,1]).dot(trans2)
        if srcPos[0] >= 0 and srcPos[0] < w and srcPos[1] >= 0 and srcPos[1] < h:
            # 最邻近内插
            newimg2[y][x] = img[int(srcPos[1])][int(srcPos[0])]
            # 双线性内插
            bix,biy = int(srcPos[0]),int(srcPos[1]) # 取左上角坐标
            # 避免最后一行溢出
            if bix < w-1 and biy < h-1:
                # 沿 X 方向线性内插
                rgbX1 = img[biy][bix] + (img[biy][bix+1] - img[biy][bix])*(srcPos[0]-bix)
                rgbX2 = img[biy+1][bix] + (img[biy+1][bix+1] - img[biy+1][bix])*(srcPos[0]-bix)
                # 沿 Y  方向内插
                rgb = rgbX1 + (rgbX2-rgbX1)*(srcPos[1]-biy)
                newimg3[y][x] = rgb
# 绘图
sub = plt.subplot(2,2,1)
sub.set_title("Src Img")
plt.imshow(img)
sub = plt.subplot(2,2,2)
sub.set_title("Src->Des")
plt.imshow(newimg1)
sub = plt.subplot(2,2,3)
sub.set_title("Des->Src & Nearest")
plt.imshow(newimg2)
sub = plt.subplot(2,2,4)
sub.set_title("Des->Src & Bilinear")
plt.imshow(newimg3)
plt.show()

效果图展示

可以看出来双线性比最邻近好的多了