最短路径的三种算法以及路径还原与负圈判断

发表于 分类于 ， 阅读次数： 本文字数： 2.5k 阅读时长 ≈ 9 分钟

图的基础，最短路径的几种解答

单源最短路： Bellman-Ford & Dijkstra 及其简单优化 以及负圈的判断

多源最短路：Floyd-Warshall 算法的简单理解

路径还原问题

算法代码及思路主要参考：《挑战程序设计竞赛》

在此之前读者应对图已经有基础的概念，以及图的邻接表 & 邻接矩阵的表示方法

Bellman-Ford

单源最短路问题是固定一个起点，然后求这个点到其他各个顶点的最短路（最小权值和）

设起点 s 到其他顶点 i 的距离为 d[i] 则很容易可以得到下面这个结论： \[ d[i] = min\{d[j] + edge(j,i)\} \quad edge(j,i) \in E \] 设置初始状态 d[s] = 0 else d[i] = INF 然后只要在循环里不断更新这些值

如果不再更新说明所有路都已达到最短 代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
struct Edge{ int from, to, cost;}; // 定义从点from指向to权值为cost的边
Edge edges[MAXN];

int d[MAXN]; // 最短距离
int V,E; // V: 顶点数 E: 边数

// 从点s到其他点的最小距离
void Bellman_Ford(int s)
{
    for(int i = 0;i < V;i++) d[i] = INF;
    d[s] = 0; // 到自己为0
    while(true)
    {
        bool isUpdate = false;
        for(int i = 0; i < E; i++)
        {
            Edge temp = edges[i];
            if(d[temp.from] != INF && d[temp.to] > d[temp.from]+temp.cost)
            {
                d[temp.to] = d[temp.from] + temp.cost;
                isUpdate = true;
            }
        }
        if(!isUpdate) break;
    }
}

如果图中不存在 s 可达的负圈，那么最短路不会经过一个顶点两次，也就是说 最多通过 V-1 条边，也可以这样理

解，每一次更新都会有更短的路径产生，那么在 V 个点的图中，两个点的最远距离只能是 V-1 条边，所以循环最多

只会执行 V-1 次，这个特性将是我们判断是否存在负圈的重要性质

所以我们也可以将上面的代码简单化为：

1
2
3
4
5
6
7
8
9
10
11
12
13
void Bellman_Ford(int s) // 不存在负圈的情况
{
    for(int i = 0;i < V;i++) d[i] = INF;
    d[s] = 0; // 到自己为0
    for(int j = 0;j < V-1;j++)
    {
        for(int i = 0; i < E; i++)
        {
            Edge temp = edges[i];
            d[temp.to] = min(d[temp.to],d[temp.from]+temp.cost)
        }
    }
}

很容易可以看出来 Bellman 算法的复杂度为 O(V*E)

负圈的判断

在这里，首先要明确负圈（负权环）和负权边的区别

负圈是指一条环状路径上的综合权值为负的，负权边是指权值为负数的边，在算法中如果图是无向图的话，

负权边和负圈是等价的。如下图：也就是在A与B之间形成了一个环，这个环的权值为-2

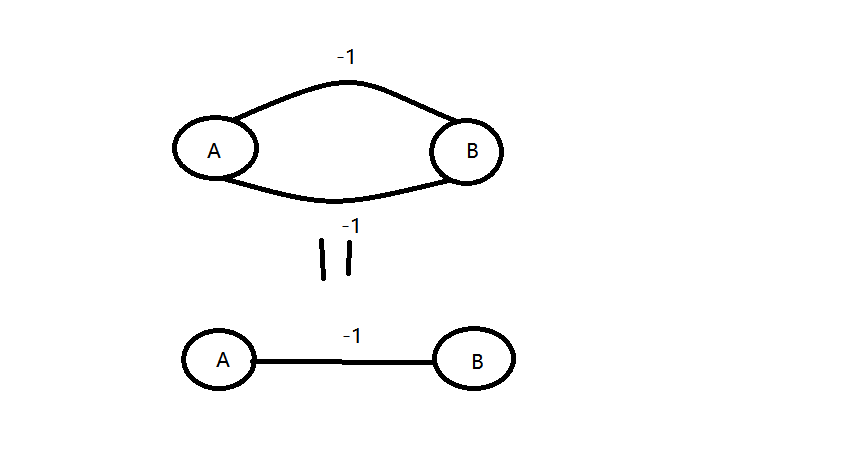
所以在无向图中负边的存在也就是负圈的存在。所以Bellman主要是可以用来判断有向图中是否存在负圈。

只要存在了负圈，那么 Bellman 的松弛操作（也就是那个每次更新的内容）将会永远的执行下去。

相当于没走一个这个负圈总的权值（路径长度）就会减少。但是我们上面已经得到在不存在负圈的图中最多执行 V-1 次循环，所以我们只要判断在第V次仍然更新了，那么就存在负圈了。代码只要更改一点点就行：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void Bellman_Ford(int s) // 不存在负圈的情况
{
    for(int i = 0;i < V;i++) d[i] = INF;
    d[s] = 0; // 到自己为0
    for(int j = 0;j < V;j++)
    {
        for(int i = 0; i < E; i++)
        {
            Edge temp = edges[i];
            if(d[temp.from] != INF && d[temp.to] > d[temp.from]+temp.cost)
            {
                d[temp.to] = d[temp.from] + temp.cost;
                // 只要再次加上到第V-1次的特判
                if(j == V-1)
                {
                    cout << "存在负圈" << endl;
                    return;
                }
            }
        }
    }
}

Dijkstra

我们先考虑不存在负边的情况，在 Bellman 算法中每一次都要全部遍历所有的边，而且如果d[i]本身不是最短路径

那么进行那个松弛操作之后的 d[i] 依然不是最短，所以可以对此进行优化：

  • 找到最短路径已经确定的顶点，更新从他出发相邻顶点的最短距离

  • 从此不需要在更新上面已经确定的哪些顶点（即不需要遍历）

这就衍生出了 Dijkstra 算法。上面两点用图来描述就是：

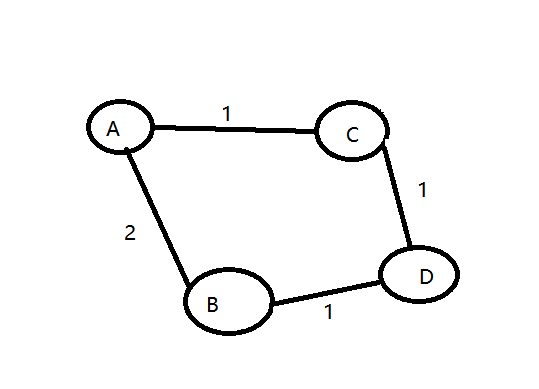
假设初始点为 A 首先 AC < AB

很清楚的我们可以得出结论 AC 就是A到C的最短路径，因为如果从 AB 方向走的话，AB ＞AC 而且我们的图是没有负边的，所以 BD > 0 也就是说 AB + BD.... > AC 是必然成立的。 所以 A->C 的最短路径已经确定了，之后就需要再去管C点了。算法总的描述如下：

在最开始时，只有起点的最短距离是确定的（而且所有点都未曾使用）。而在尚未使用的顶点中，距离d[i]最小的顶点就是最短距离已经确定的顶点。因为不存在负边，所以 d[i] 不会在以后的更新中变小。这就是 Dijkstra 算法

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
int cost[MAXN][MAXN]; // cost[i][j] 表示从i到j之间的权值（不存在是为INF）
int d[MAXN]; // 从起点到其他点的最短距离
bool used[MAXN]; // 已经使用过的图（已经确定最短距离的点）
int V; // 点的个数

void Dijkstra(int s)
{
    fill(d,d+V,INF); // algorithm中的函数 将d数组全部赋为INF
    fill(used,used+V,false);
    d[s] = 0;
    
    while(true)    
    {
        int v = -1;
        // c从未使用过的点集中取一个距离最小的点
        for(int u = 0;u < V;u++)
        	if(!used[u] && (v == -1 || d[u] < d[v])) v = u;
        if(v == -1) break; // 所有的点的最短路径确定则退出
       	used[v] = true;
        for(int u = 0;u < V;u++)
        {
            d[u] = min(d[u],d[v]+cost[v][u]);
        }
    }
}

简单的优化

上面代码的时间复杂度是 O(V2) , 我们可以通过堆（优先队列）降为O(E*log(V))

上面有一个操作是找到距离最小的点和标记是否使用，这个就可以使用堆来优化

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
typedef pair<int,int> P; // first 是最短距离 second 是顶点编号
struct edge{int to, cost};
vector<edge> G[MAXN]; // 使用邻接表存图
int d[MAXN]; // 从起点到其他点的最短距离
bool used[MAXN]; // 已经使用过的图（已经确定最短距离的点）
int V; // 点的个数

void Dijkstra(int s)
{
    priority_queue<P,vector<P>, greater<P> > que; // 定义一个堆 从按最短距离小到的大排
    fill(d,d+V,INF);
    d[s] = 0;
    que.push(P(0,s));
    while(!que.empty()) // 为空就说明所有节点都已经用过
    {
        P temp = que.top(); que.pop();
        int v = temp.second;
        if(d[v] < temp.first) continue; // 没必要更新了
        for(int i = 0;i < G[v].size();i++)
        {
            edge e = G[v][i];
            if(d[e.to] > d[v]+e.cost)
            {
                d[e.to] = d[v]+e.cost;
                que.push(P(d[e.to],e.to));
            }
        }
    }
}

Floyd-Warshall

Floyd算法简单暴力，主要用于求多源最短路径（任意两个点的最短路径）

核心代码十分短小精悍

1
2
3
4
5
6
7
8
9
10
int d[MAXN][MAXN]; // d[u][v] 表示从u -> v的权值 不存在的时候为0
int V; // 顶点个数

void Floyd()
{
    for(int k = 0;k < V;k++)
        for(int i = 0;i < V;i++)
            for(int j = 0;j < V;j++)
                d[i][j] = min(d[i][j],d[i][k]+d[k][j]);
}

十分暴力复杂度可想而知O(V3)

那么这几行代码是什么意思呢？ 这其实还是 DP

我们用 d[k+1][i][j] 来表示只使用 0~k和 i,j 顶点的情况下的最短路

初始状态为 d[0][i][j] = cost[i][j] 所以我们可以得到下面这个式子： \[ d[k][i][j] = \begin{cases} d[k-1][i][j] 　(不经过点K)\\ d[k-1][i][k] + d[k-1][k][j]　（经过K点）\\ \end{cases}　＝　min(d[k-1][i][j],d[k-1][i][k] + d[k-1][k][j]) \] 当然 我们可以稍微优化一下，时间以及到极限了，我们可以想办法把空间复杂度降下来

也就是我们上面那个形式，也就是为什么 K 必须放在最外面的原因

我们观察三维的那个式子与K相关的就只有 K 与 K-1 所以我们可以进行降维操作

也就是当K=s的时候，在执行状态压缩之前 d[i][j] 的值存都是的 d[k-1][i][j]

也就是将上一个状态动态保存起来了 所以才有上面的简短的代码

路径还原

最后的问题就是当我们知道最短路径多少的时候，难免有时候需要知道该怎么走才有这条最短路径呢

用 Dijkstra 来演示路径还原 其他的算法也都可以用这个来解决

在此算法中满足 d[j] = d[k] + cost[k][j]的点K我们称为j的前驱结点，也就是在到j之前必须经过点K

我们用一个数组 prev 来存相应节点的前驱结点，不断寻找前驱结点就可以找到最短路了，不过这是从后往前找，最后需要反转一下得到最后的答案。

示例代码如下： 注意第25行

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
int cost[MAXN][MAXN]; // cost[i][j] 表示从i到j之间的权值（不存在是为INF）
int d[MAXN]; // 从起点到其他点的最短距离
bool used[MAXN]; // 已经使用过的图（已经确定最短距离的点）
int V; // 点的个数
int prev[MAXN];

void Dijkstra(int s)
{
    fill(d,d+V,INF); // algorithm中的函数 将d数组全部赋为INF
    fill(used,used+V,false);
    fill(prev,prev+V,-1); // -1表示到头了 即没有前驱结点
    d[s] = 0;
    
    while(true)    
    {
        int v = -1;
        // c从未使用过的点集中取一个距离最小的点
        for(int u = 0;u < V;u++)
        	if(!used[u] && (v == -1 || d[u] < d[v])) v = u;
        if(v == -1) break; // 所有的点的最短路径确定则退出
       	used[v] = true;
        for(int u = 0;u < V;u++)
        {
            d[u] = min(d[u],d[v]+cost[v][u]);
            prev[u] = v; 
        }
    }
}

// 到顶点t的最短路
vector<int> get_path(int t) 
{
    vector<int> path;
    for(; t != -1;t = prev[t]) path.push_pack(t);
    reverse(path.begin(),path.end());
    return path;
}

The end !!!