一些我们在英语论文写作过程中容易犯的错误以及注意点。

以下内容摘自：The Most Common Habits from more than 200 English Papers written by Graduate Chinese Engineering Students

Linux/Unix 入门编程手册，参考自 《Linux/Unix 系统编程手册》Michael Kerrisk 著。

主要对 Linux/Unix 下文件、信号、进程、线程、IPC 等作简要描述。

篇幅较多，单独收录到：Readme - Linux/Unix 入门编程 (weijun-lin.top)

上次更新: 2023-10-01

不断补充中……

SFM Learner 2017

Zhou T, Brown M, Snavely N, et al. Unsupervised learning of depth and ego-motion from video

为单目深度估计与相机姿态估计提出完全无监督的学习框架；

单视图深度估计与多视图位姿分别构建网络，将图像变换到目标视图上以构建损失，并根据此损失训练网络

非线性优化普遍的解决思路是使用非线性最小二乘，非线性最小二乘可参考前一篇文章“相机位姿估计”。在很多优化过程中，如果优化变量本身具有一定的约束，这样的优化将变得十分复杂，所以如果能将约束问题转换为无约束的这可以带来极大的便利。在高翔博士的《SLAM 十四讲》中，其中的 BA 优化便利用李群李代数构造旋转矩阵的无约束优化问题，这在博客“相机位姿估计”中也比较详细介绍了。这里记录一下对流形优化新的思考。

一、 研究问题

在基于视觉的三维重建算法（如 Structure From Motion, SFM¹）以及同时定位与地图构建（Simultaneous localization and mapping, SLAM²³）等涉及立体视觉的理论研究中，需要通过相机成像模型及特征点匹配等理论恢复相机位姿以重构三维场景，即目标点云的生成。

相机的位姿估计指从若干给定的图像中恢复相机的运动（位姿），进而恢复目标的三维结构（点云）。相机运动（位姿）即相机的外部参数，是世界坐标系到相机坐标系的变换，包含旋转和平移，即欧式变换。相机成像模型如下： \[ ZP_{uv} = Z \left[ \begin{matrix} u \\ v \\ 1 \end{matrix} \right] = K(RP_w+t) = KTP_w \tag{1.1} \]

其中 \(Z\) 为世界坐标系下目标点 \(P_w\) 的 z 轴坐标，\(K\) 为相机内参，可通过张正友标定法⁴确定，\(R,t\) 为世界坐标系到相机坐标系的变换，可以使用矩阵 \(T\) 表示，\(P_{uv}\) 代表像素坐标系，\(u,v\) 为像素坐标。这里目标为通过一些约束估计相机外参 \(R,t\) 。获取相机位姿后便可以进一步得到目标的三维点云。

当代中国社会各阶级（阶层）分析？ - Hac棱镜的回答 - 知乎

1925年冬 ，毛选首卷首篇落成 ，中国社会各阶级的分析 。落笔如刀，将当时中国社会一分为六，寥寥数千字，写尽四万万人。疏忽百年，斯人长逝，时移事迁，请以新作，再论当下之中国。

一些介绍马氏距离比较好的文章：

• 马氏距离(Mahalanobis Distance) - 知乎 (zhihu.com)
• 理解向量空间变化：马氏距离 - 知乎 (zhihu.com)
• 如何理解马氏距离，多维Mahalanobis距离是否要用到“互相关张量”来进行描述？ - 快使用双截棍巴拉的回答 - 知乎
• 欧式距离、标准化欧式距离、马氏距离、余弦距离_一只飞鱼的博客-CSDN博客_欧式距离

这里主要做一个补充

很现实，很慵懒，不能逃避，只能面对

原文：Evaluating The Performance Of Structure From Motion Pipelines

摘要：运动中恢复结构是一个通过一组图片集实现三维重建的管线。一个经典的 SFM 管线将多个步骤组合在一起，每一个步骤处理不同的问题。并且每一个步骤可以使用不同的算法，因此可以建立许多不同的 SFM 算法。为不同的人物选择合适的 SFM 算法是一个很重要的问题。在这篇文章中，我们根据重建不同场景的能力，对较新的 SFM 管线做了比较。我们还提出了一个评估程序，使用高级设备获取的真实场景图像以及真实的合成数据集对 SFM 管线进行评估。最后，我们为 Blender 创建了一个插件来为合成数据集创建以及 SFM 管线评估提供支持。合成数据集的使用使得我们容易地获取大量并且不同的数据集，理论上和真实图像无限接近。我们的评估程序不仅考虑了重建误差，还考虑了用于重建的相机姿态误差。

关键词： SFM，三维重建，Blender，评估

小结

晃眼四年已过
仔细想想
仿佛昨天还在青广翻着行李箱
急急忙忙找着报到需要的证件

相机模型

《CV中的多视图几何》——再谈相机模型 - 知乎 (zhihu.com)

An Introduction to Epipolar Geometry | Sanyam Kapoor (perhapsbay.es)

小孔相机是相机模型的简化，小孔与成像平面之间的距离称为焦距。一般来说，小孔越小成像越清晰，但太小会造成衍射，导致成像模糊。

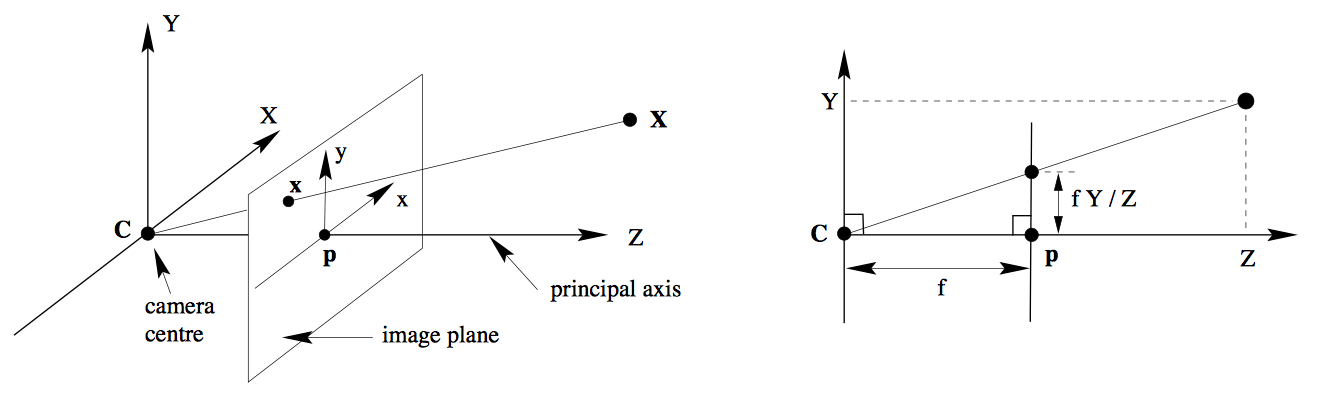
由相似三角形可得，空间上一点 \((X,Y,Z)\) 在成像平面上的点为：\((f\frac{X}{Z},f\frac{Y}{Z})\)，矩阵表达如下： \[ \left( \begin{matrix} fX\\ fY\\ Z \end{matrix} \right) = \left[ \begin{matrix} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{matrix} \right] \left( \begin{matrix} X \\ Y \\ Z\\ 1 \end{matrix} \right) \tag{1} \] 即 \(\mathbf{x} = P\mathbf{X}\)，需要注意的是，这里矩阵相乘的结果还需要除以第三个分量的 \(Z\) 才为真正的图像平面坐标（齐次化），即 \(\bf x\) 为摄像机坐标系下的坐标，除以第三个分量为图像坐标系下的点，即像素点，其中矩阵： \[ K = \left[ \begin{matrix} f_x & s & p_x \\ 0 & f_y & p_y \\ 0 & 0 & 1 \end{matrix} \right] \] 为相机内参矩阵，为式(1)矩阵的拓展，其中 \(f_x,f_y\) 表示相机像素长宽不一定一致，\(p_x,p_y\) 为成像平移，因为不一定在中心，\(s\) 为仿射畸变，即成像横纵轴不一定垂直。理想状态下相机如式(1)所示。

令 \(\bf p\) 表示图像坐标系上的点有：\(Z\mathbf{p} = \mathbf{x} = K\mathbf{X}\)，其中 \(X = (X,Y,Z)\)，归一化坐标表示为 \(\mathbf{\hat X} = (X/Z, Y/Z, 1)\)，也就是将坐标都压缩到 \(Z = 1\) 平面上。

归一化坐标和图像坐标有以下关系： \[ \begin{align} Z\mathbf{p} &= \mathbf{x} = K\mathbf{X} \\ \mathbf{p} &= K\mathbf{\hat X} \\ \mathbf{\hat X} &= K^{-1}\mathbf{p} \tag 2 \end{align} \]

关键词：三维重建；图像；稀疏点云重建（SFM）；稠密点云重建（MVS）；评价指标

下载链接

获取三维模型主要通过以下三种方式：

1. 传统的几何建模技术

   最为成熟，但周期长，操作复杂

2. 基于图像的三维重建

   基于多幅不同角度拍摄的图像，运用计算机视觉理论进行三维建模；也有基于单幅图像的，但不能用于大规模场景

3. 基于点云的三维重建

   利用三维扫描设备对目标进行扫描，以重建模型

文章主要介绍基于多幅图像的三维重建算法，主要包括稀疏点云重建（Structure From Motion，SFM）；稠密点云重建（Multi-View System，MVS）。其中 SFM 包括特征点检测与匹配（SIFT，SURF，FAST等）以及 SFM 重构两个部分。

SFM 重构大致分为三类：增量式重构、全局式重构、混合式重构。在 MVS 中，深度图的计算尤为重要。

图像变换中总是伴随着映射，原图中的点到新图中的点之间的映射。从原图映射到新图上，由于坐标的不连续，就有新图上某点的像素确定的问题。也就是像素坐标是整数，但是映射之后的坐标不一定是整数，就需要确定它周围的坐标的像素值。图像像素的映射有前向映射和后向映射。

后向映射比较好理解，新图映射到原图上某点，然后通过它周围的像素确定这个点的像素值，一般可以有最邻近，双线性，双三次插值等。双线性比较简单且好用。

前向映射到新图中的浮点数位置，直接取整会有空洞产生，一种合适的方法就是按双线性的思路，把这个点的像素按权值分配到四个周围整数点。直接这样累加会导致像素重叠，所以还需要最后对分配到某个像素的所有像素值及其对应权值归一化。

matlab 自带了 ransac 函数，这里总结一下用法。matlab 自带的这个函数其实是 MSAC（M-estimator sample consensus）算法，但其实差不多，它对给定数据集，以及自定的模型计算函数和误差计算函数返回具有最大内点的模型。

原文链接：As-Projective-As-Possible Image Stitching with Moving DLT

这里主要对文章的 Moving DLT 做介绍，其它关于图像拼接的细节就不描述了，文章的重点就在使用 Moving DLT 来模拟一个复杂映射

摘要：图像拼接的商用化给我们带来了这个问题已经被解决的错误印象。实际上，在某些严厉的成像条件上，这些结果都不能够使人信服，除非在只有视角旋转变化或者场景为平面的条件下。在这些约束下，可以使用二维射影变换或者单应来对齐图片。在一般情况下，这种条件经常被打破，造成错误的对齐或者鬼影。现在这些拼接技术依赖于后处理方法来消除或减轻鬼影。在这篇文章中，提出一种不同的估计技术，名为 “移动直接线性变换 (Moving DLT)”，可以优化射影变换使得其适应输入数据和理想条件的偏差。这生成了一种 尽可能投影的 的图像对齐方法，有效的减少了鬼影并且不损害透视图象拼接的几何写实性。此外，还描述了如何将这种对齐方法使用到多幅图像的大全景图生成中，通过将光束法平差（Bundle Adjustment）同时用于优化以达到准确地对齐。

关键词：图像拼接，图像对齐，射影变换，直接线性变换，移动最小二乘法